Изучение процесса e+e– ➝ KSKL
в диапазоне энергий 1.05 – 2.0 ГэВ
в с.ц.м. с детектором КМД-3
Никита Петров для семинара КМД-3 28.10.21
План презентации
- Анализ процесса e+e– ➝ KSKL
- Критерии отбора событий
- Эффективность триггеров
- Эффективность регистрации
- Радиационные поправки
- Поправка к эффективности ДК
- Сечение процесса
- Систематические ошибки
- Будущие планы
Анализ процесса e+e– ➝ KSKL
В работе использовались данные 2011, 2012, 2017, 2019 и 2020 гг. с интегралом светимости 193 пб-1.
Критерии отбора событий
KS отбираются по распаду KS ➝ π+π− специальной процедурой.
Если найдено несколько
KS, то выбирается один с массой,
ближайшей к среднемировой.
Требуется,
чтобы KS-кандидат был реконструирован по двум «хорошим» трекам.
Условия отбора «хороших» треков
- |z| < 12 см
|ρ| > 0,1 см- |p| > 40 МэВ
- Число сработавших
проволочек > 6 - χr2 < 15; χz2 < 10
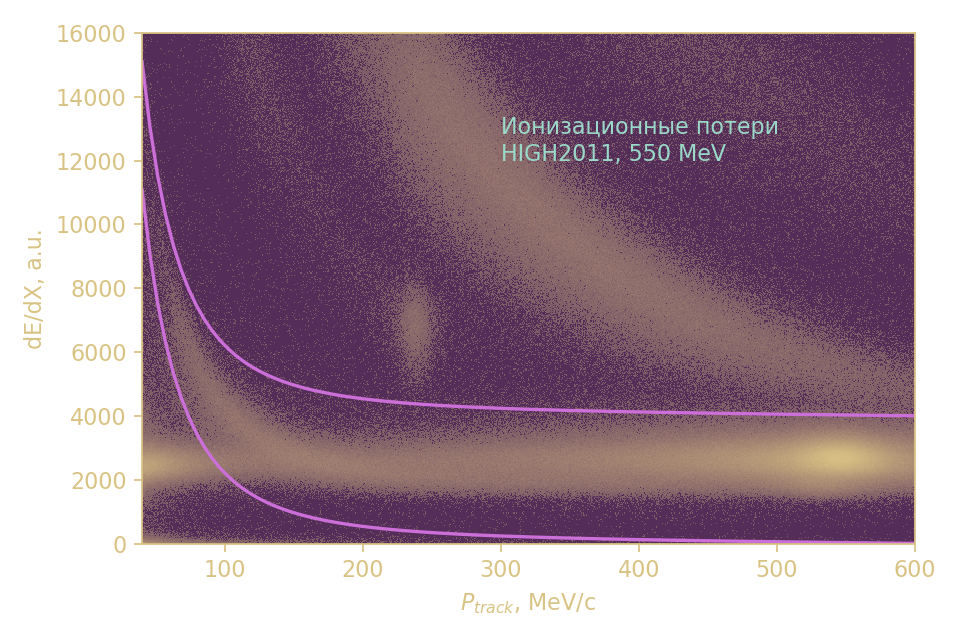
- dE/dX этих треков соответствует
ионизационным потерям пионов
Критерии отбора событий
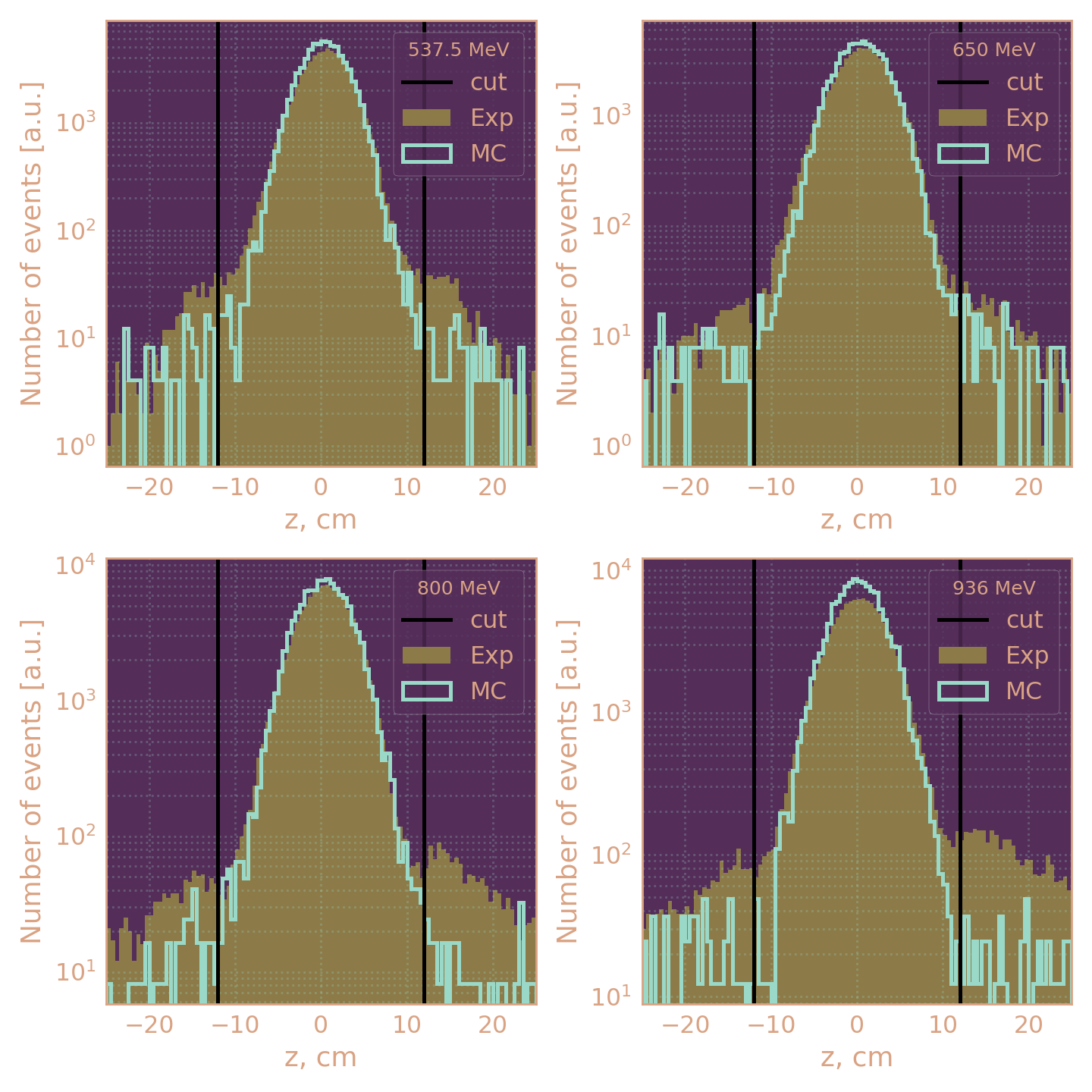
|z| < 12 см
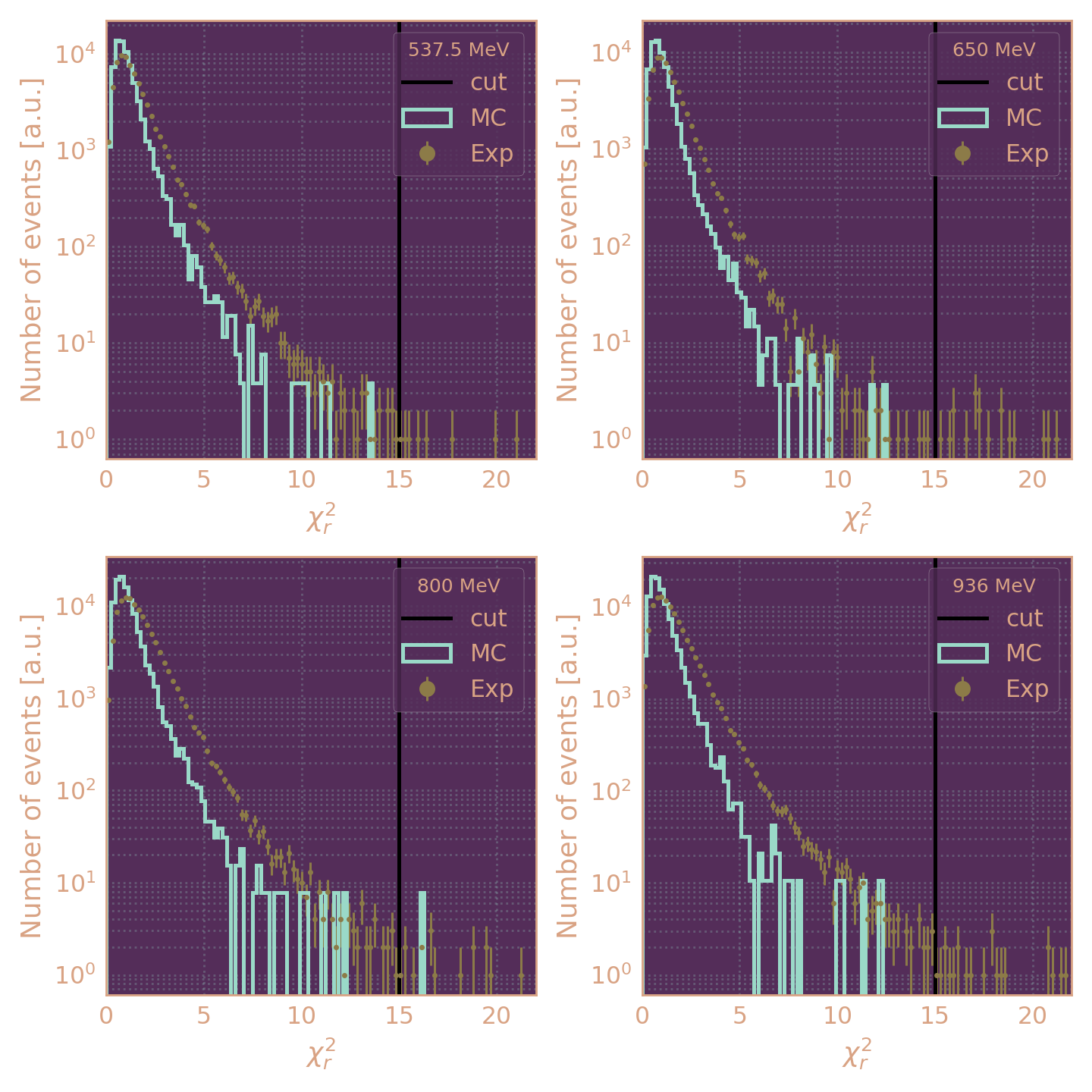
χr2 < 15
Критерии отбора событий

χr2 < 15
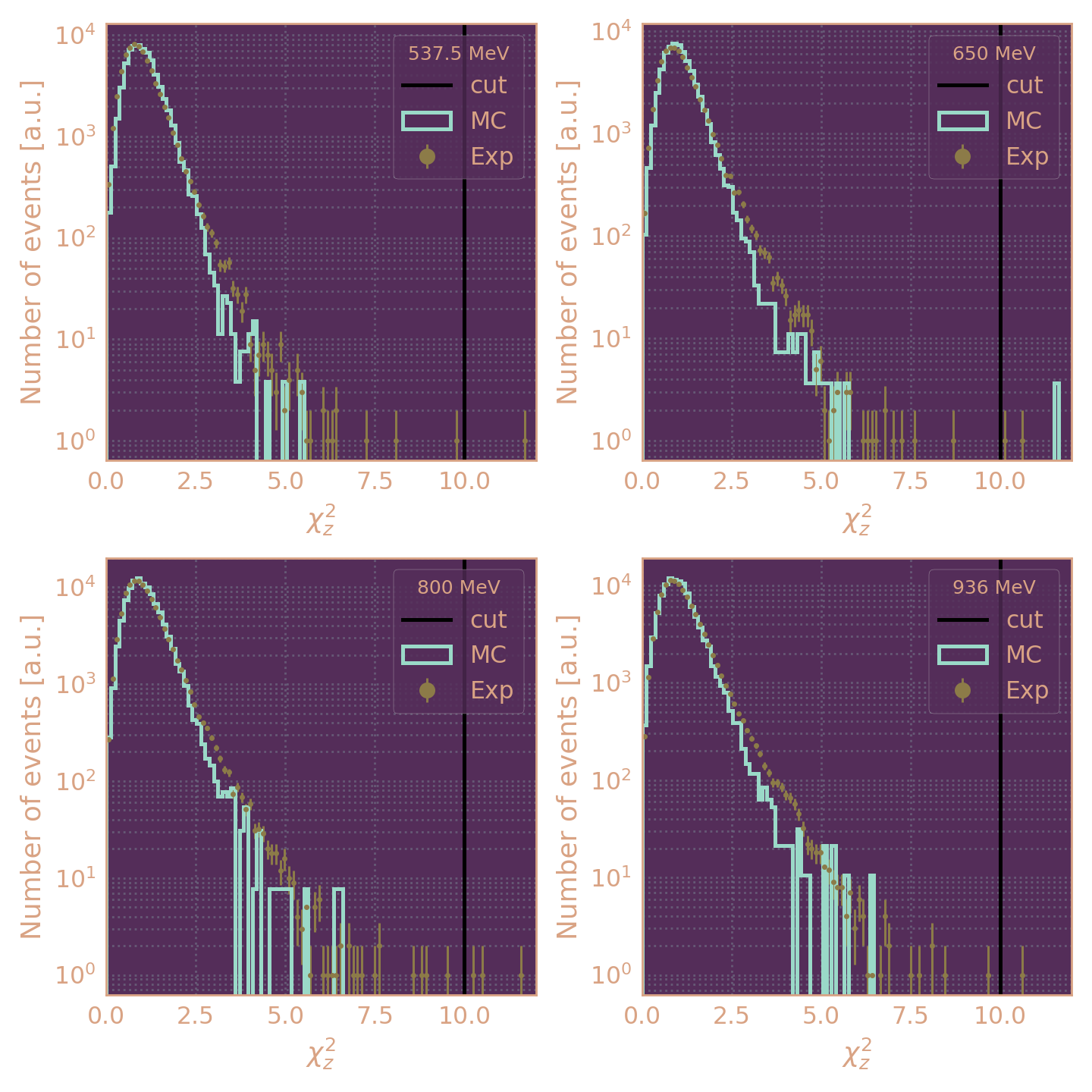
χz2 < 10
Критерии отбора событий
$$ dE/dx (\pi^{\pm}) = (161/\beta^2) \cdot \big( \ln(19275 \cdot \gamma^2 \beta^2) - \beta^2 \big) $$
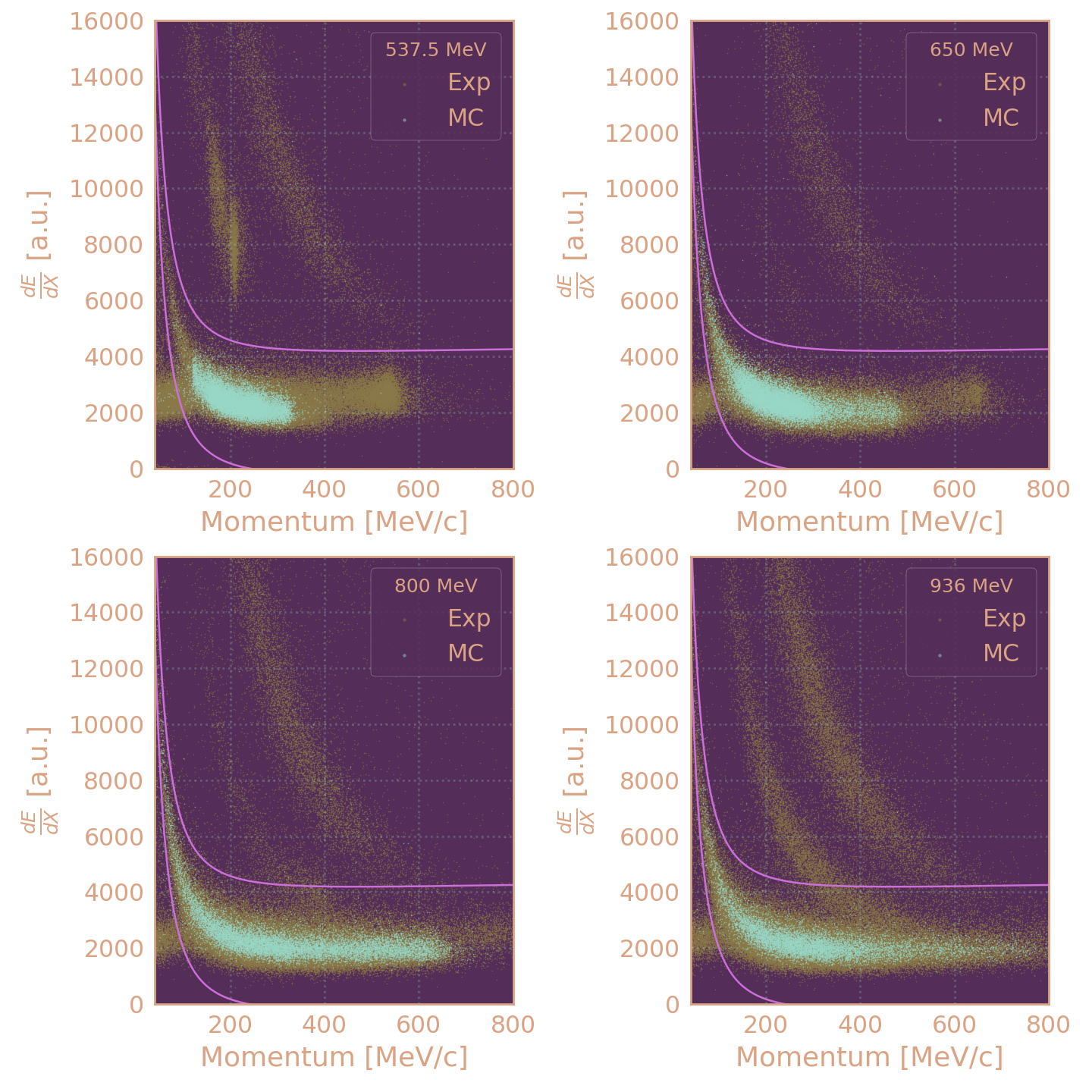
Критерии отбора событий
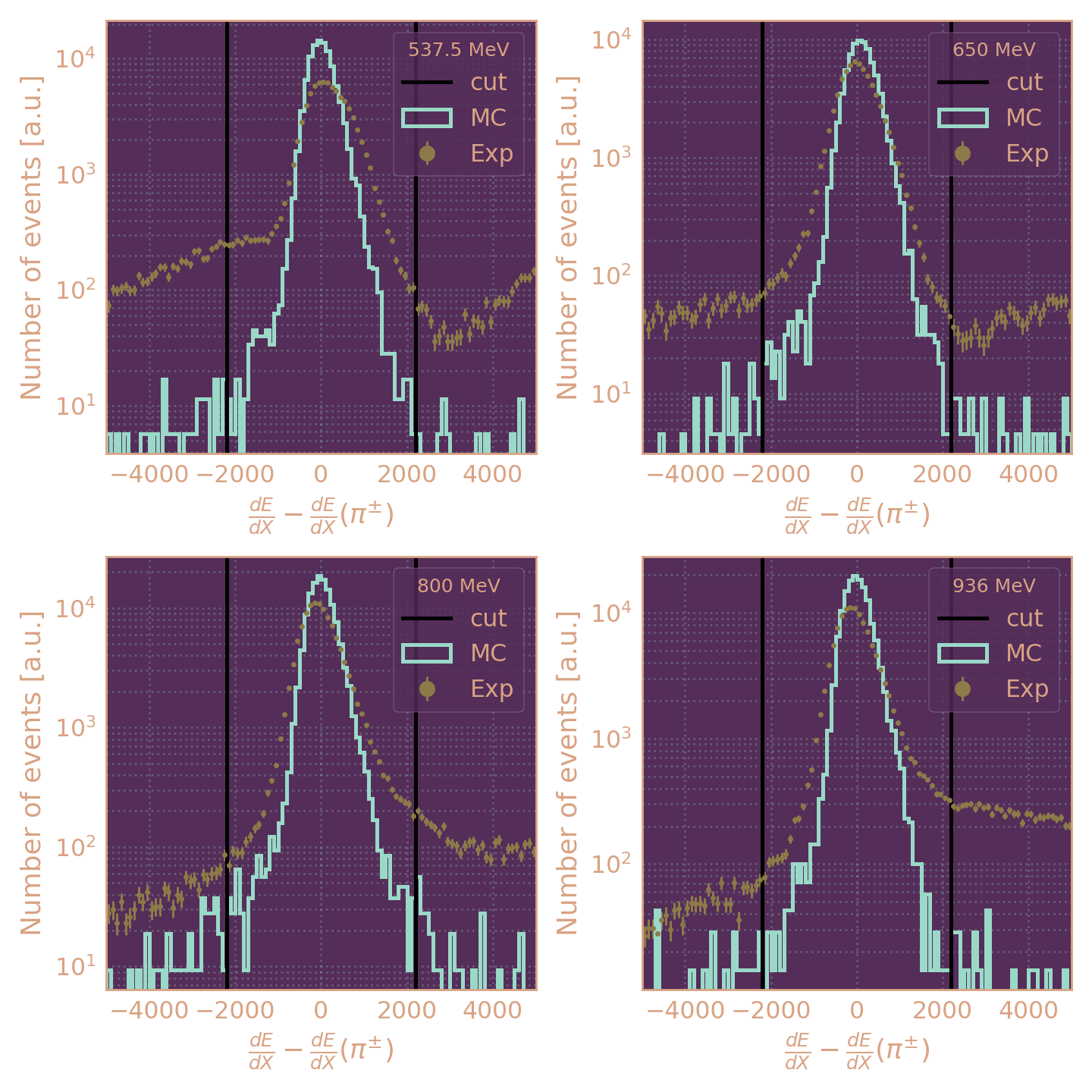
Раньше был отбор |ρ| > 0,1 см, он эффективно устраняет фон, но даёт вклад в систематику до 5%.
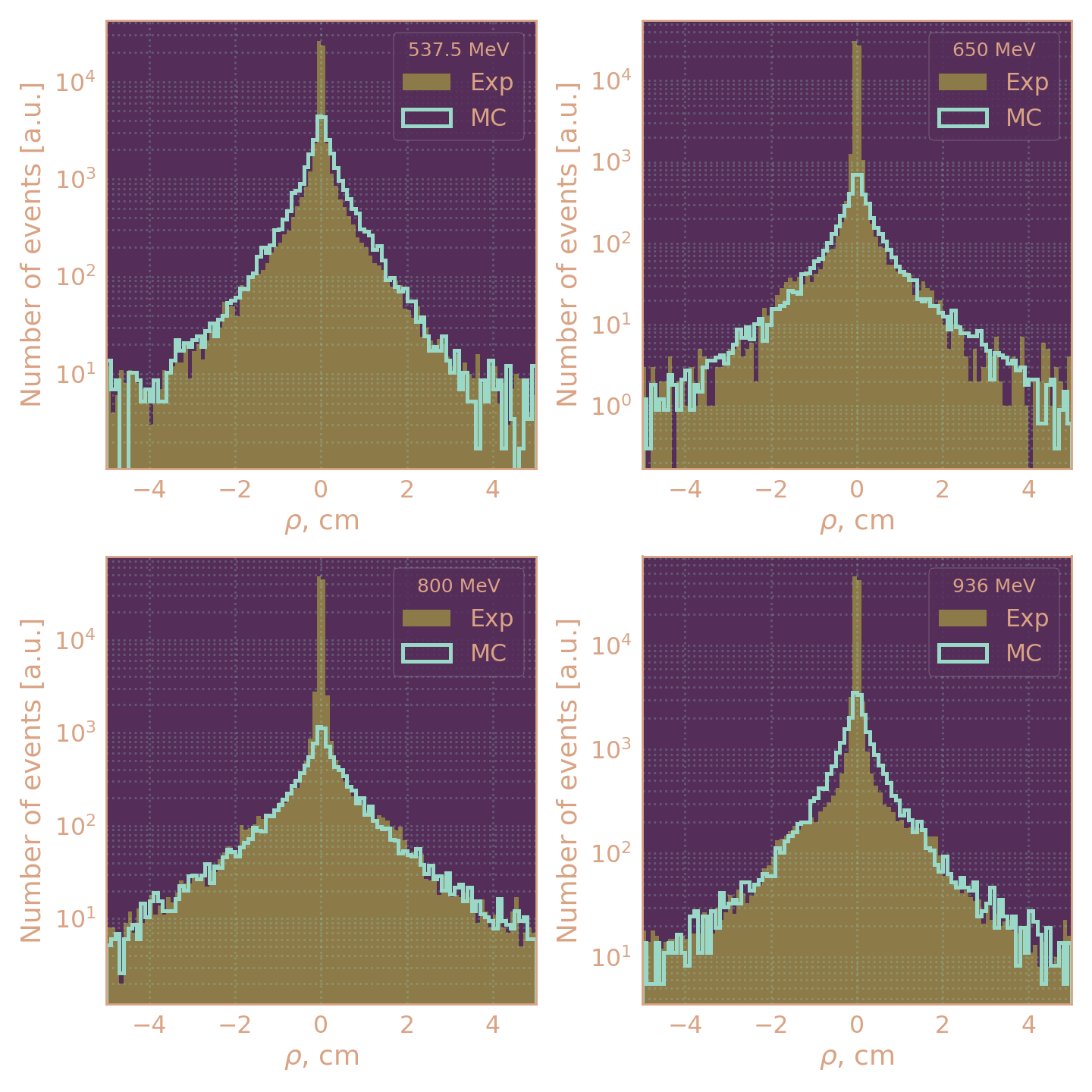
Критерии отбора событий
Отбор по углу (α < 0.64) между вектором, соединяющим место встречи пучков с вершиной распада KS, и направлением импульса KS в r-φ плоскости.
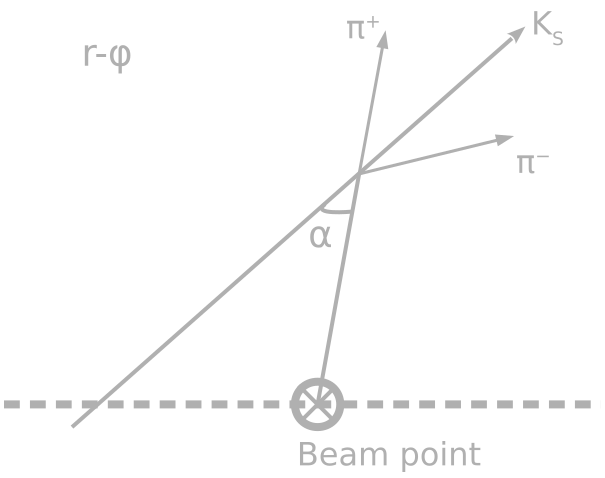
Критерии отбора событий
α < 0.64
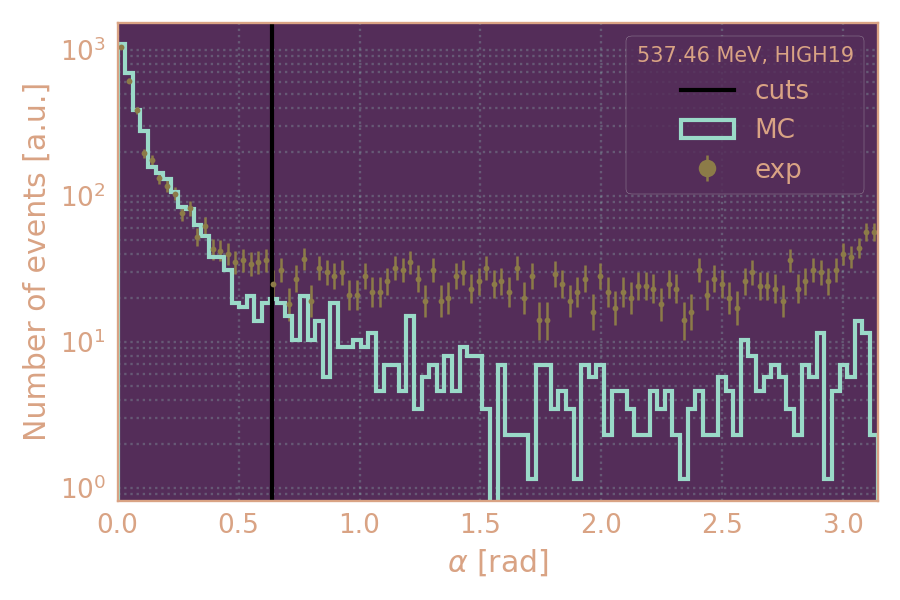
Распределение событий в эксп. и MC по углу α (HIGH19, 537.5 MeV)
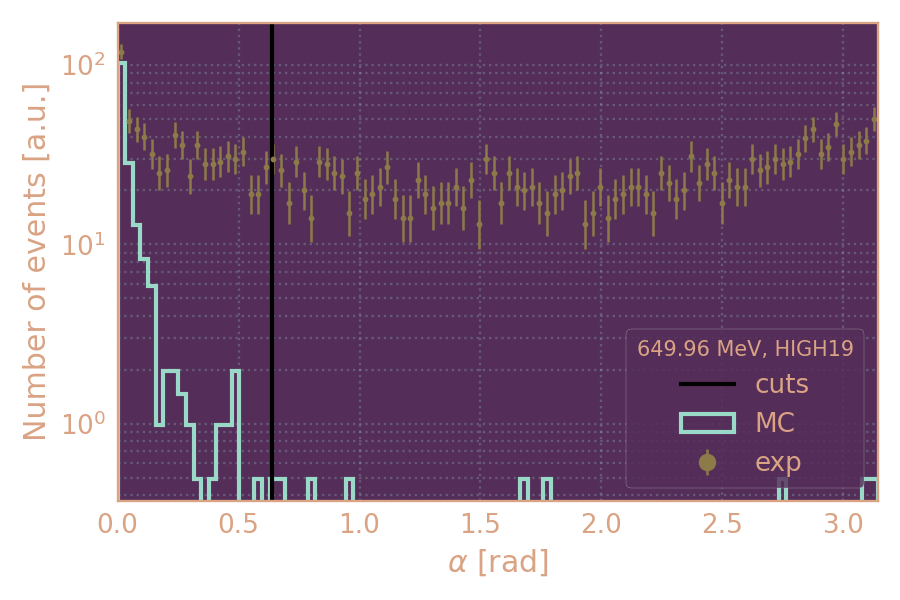
Распределение событий в эксп. и MC по углу α (HIGH19, 650 MeV)
Критерии отбора событий
α < 0.64
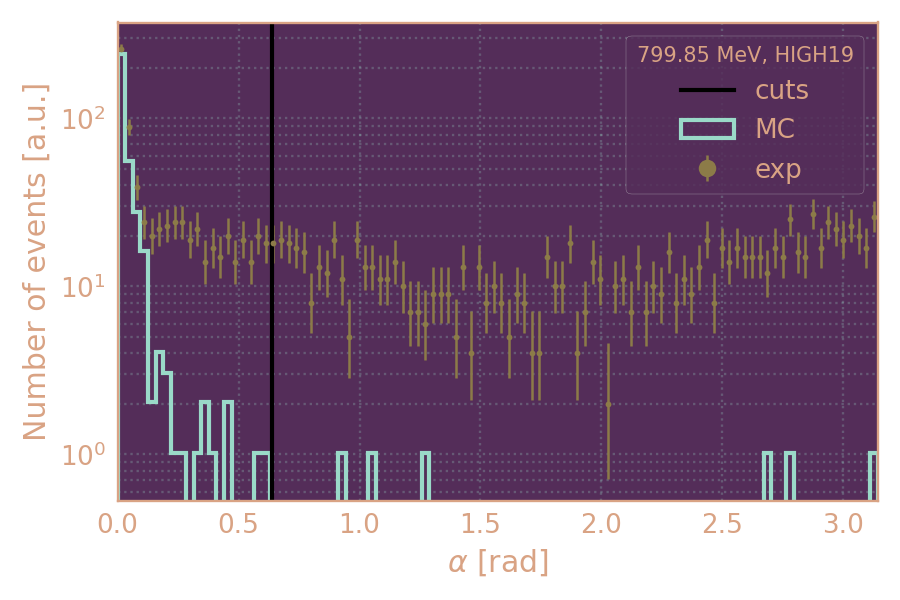
Распределение событий в эксп. и MC по углу α (HIGH19, 800 MeV)
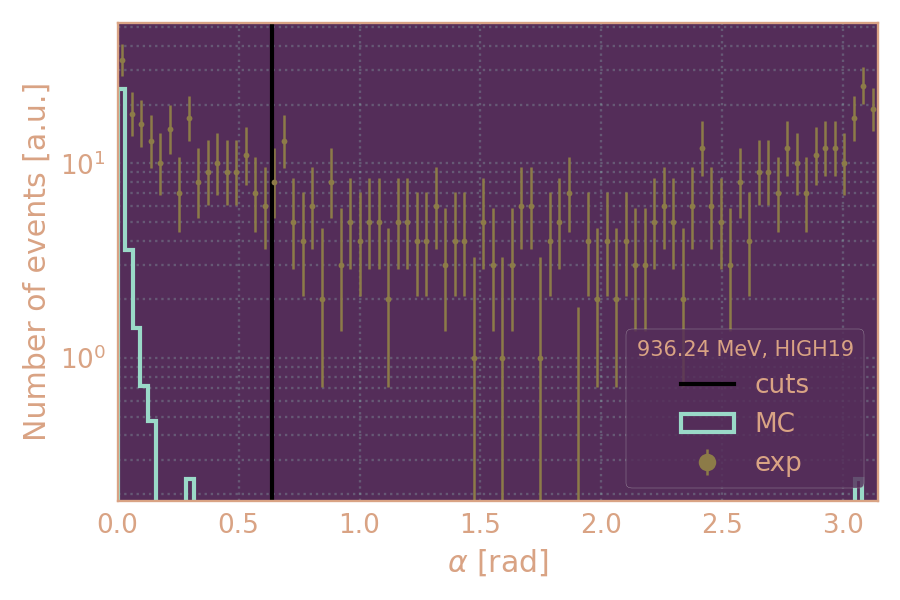
Распределение событий в эксп. и MC по углу α (HIGH19, 936 MeV)
Критерии отбора событий
Новый отбор по импульсу π± — углу разлёта распадных пионов (ψ), т.к. между ними существует связь (ЛЛ, т.2, п.11)
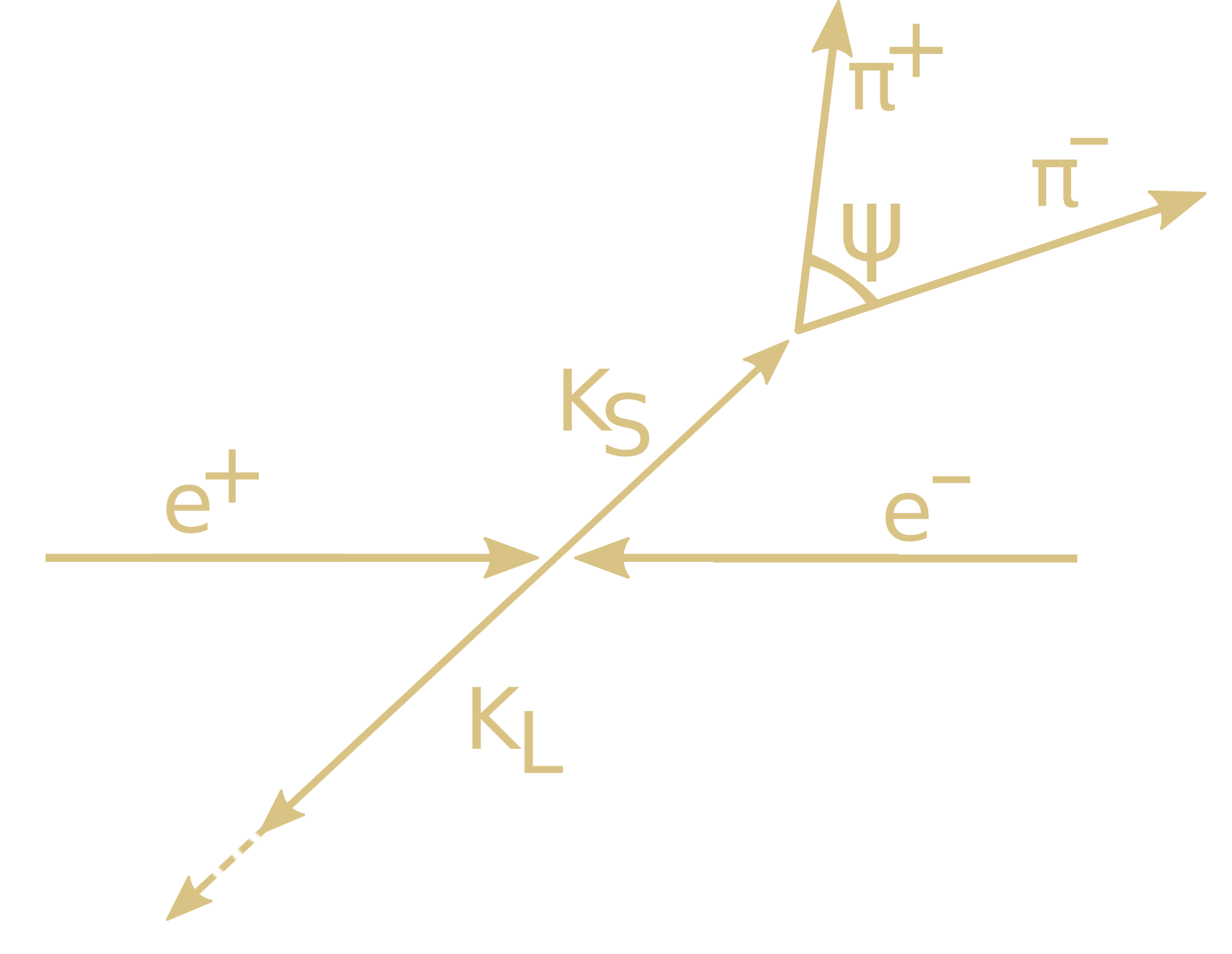
Критерии отбора событий
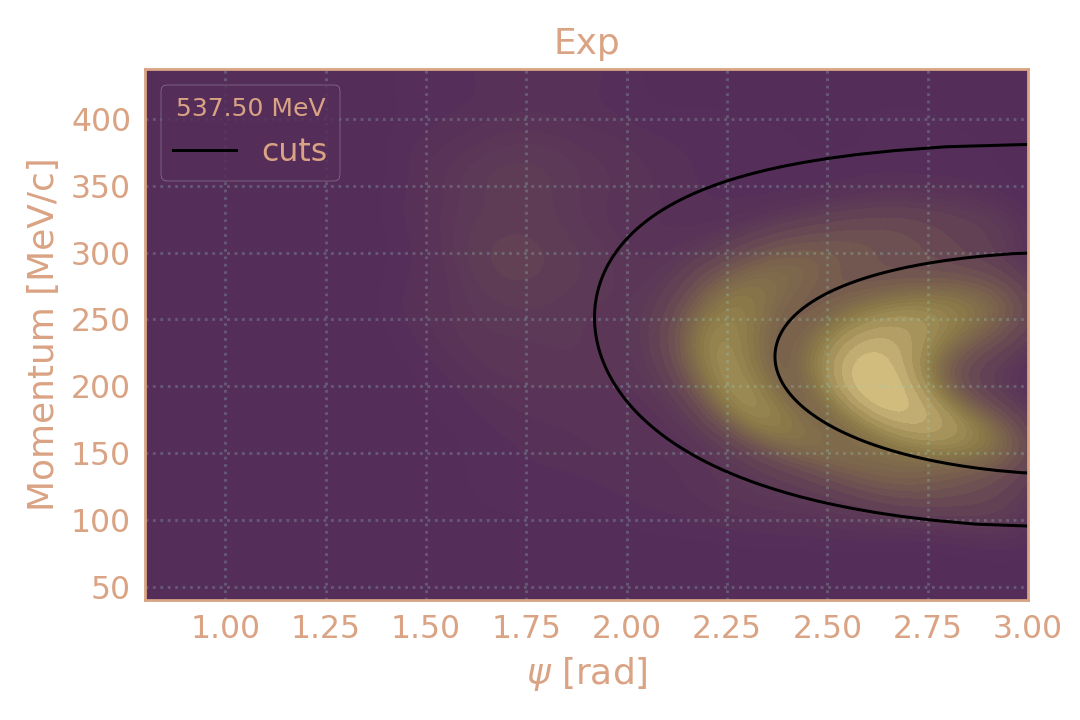
Распределение событий в эксп. (HIGH19, 537.5 MeV) по импульсу π± в зависимости от угла разлёта (ψ). Чёрным обозначены критерии отбора.
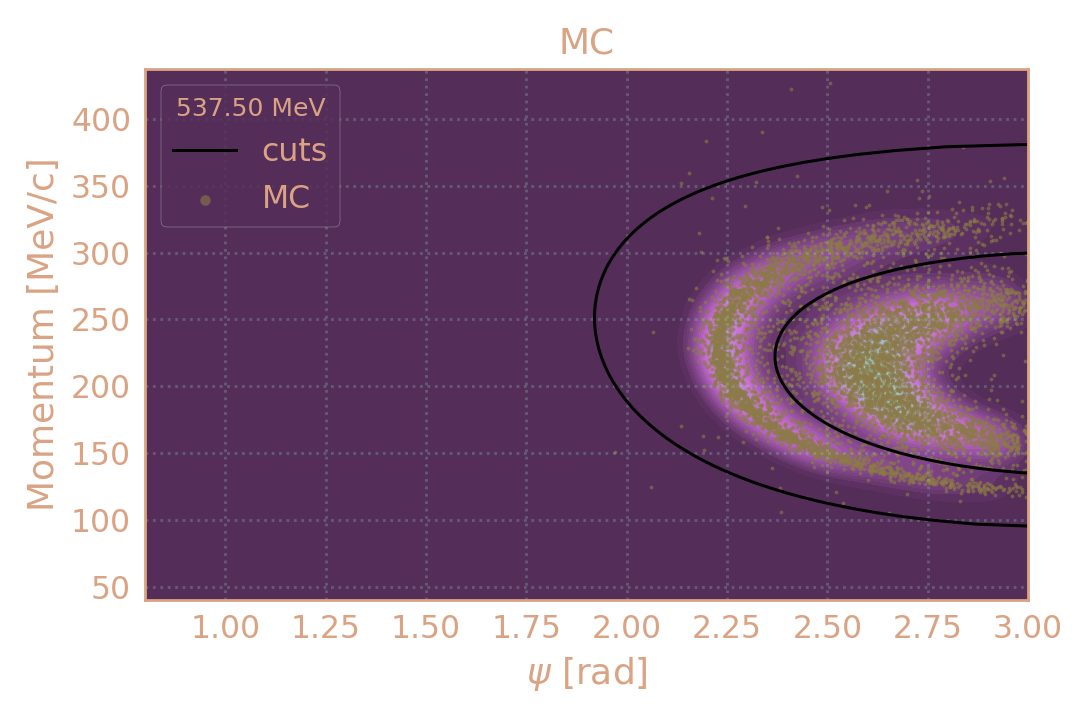
Распределение событий в MC (HIGH19, 537.5 MeV) по импульсу π± в зависимости от угла разлёта (ψ). Чёрным обозначены критерии отбора.
Критерии отбора событий
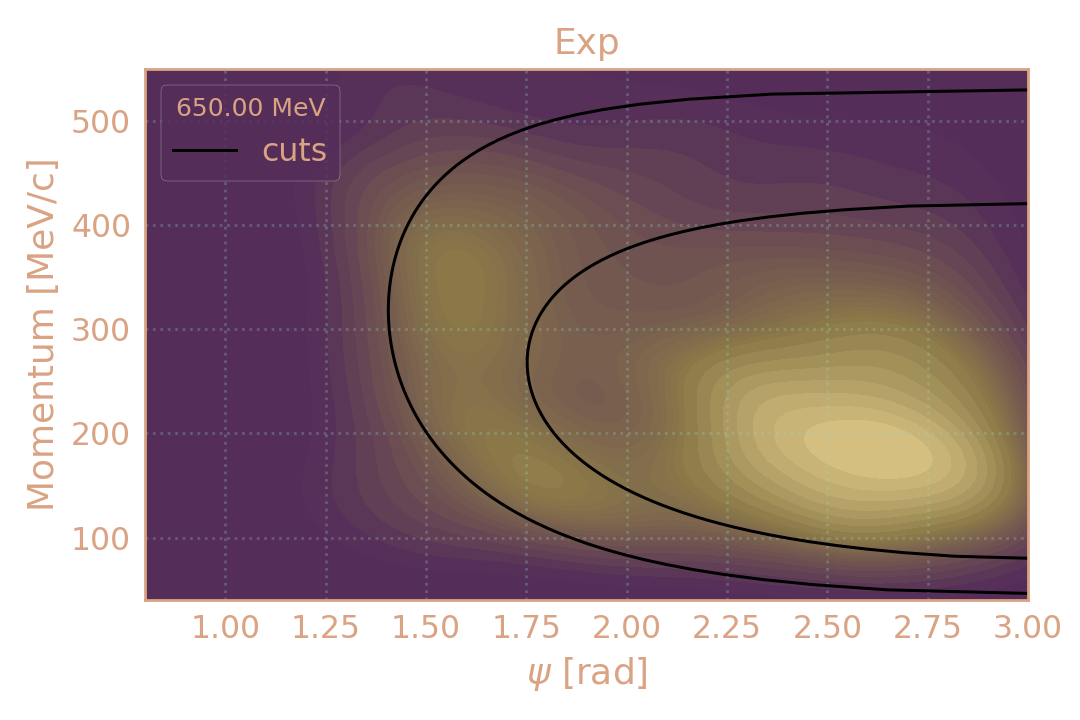
Распределение событий в эксп. (HIGH19, 650 MeV) по импульсу π± в зависимости от угла разлёта (ψ). Чёрным обозначены критерии отбора.
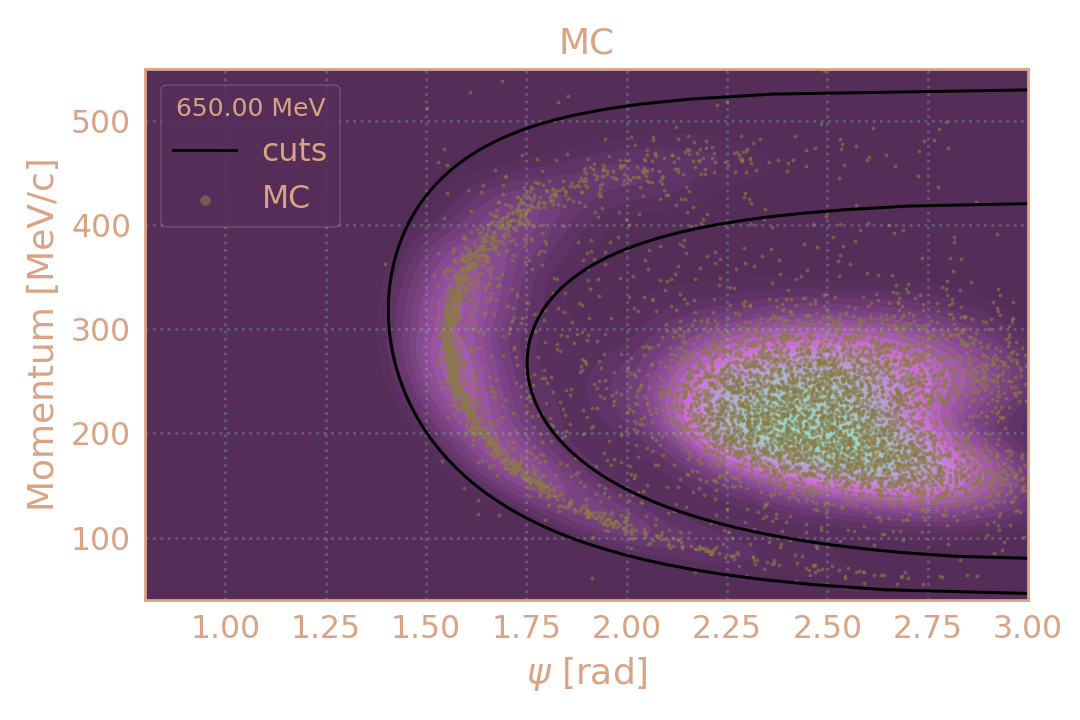
Распределение событий в MC (HIGH19, 650 MeV) по импульсу π± в зависимости от угла разлёта (ψ). Чёрным обозначены критерии отбора.
Критерии отбора событий
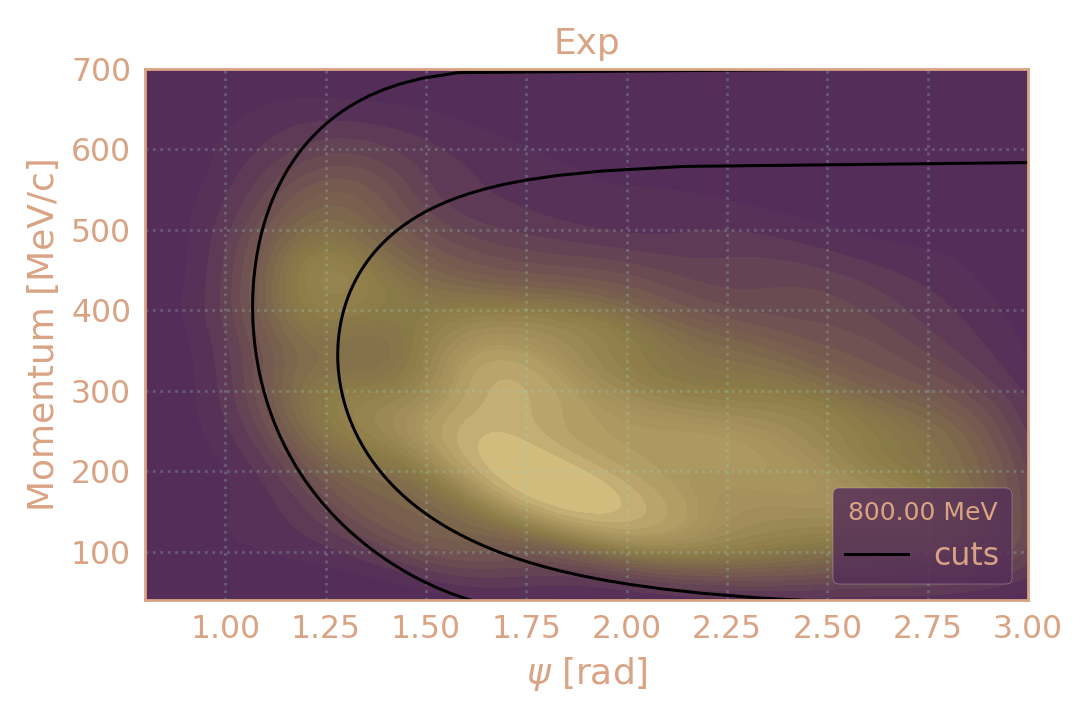
Распределение событий в эксп. (HIGH19, 800 MeV) по импульсу π± в зависимости от угла разлёта (ψ). Чёрным обозначены критерии отбора.
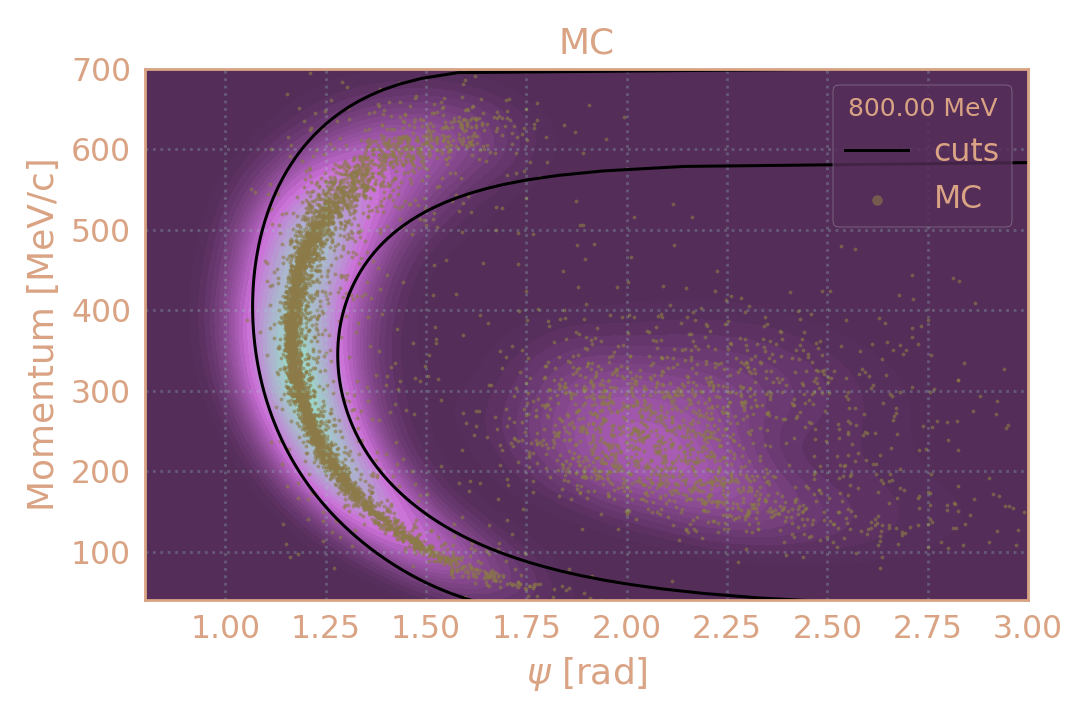
Распределение событий в MC (HIGH19, 800 MeV) по импульсу π± в зависимости от угла разлёта (ψ). Чёрным обозначены критерии отбора.
Критерии отбора событий
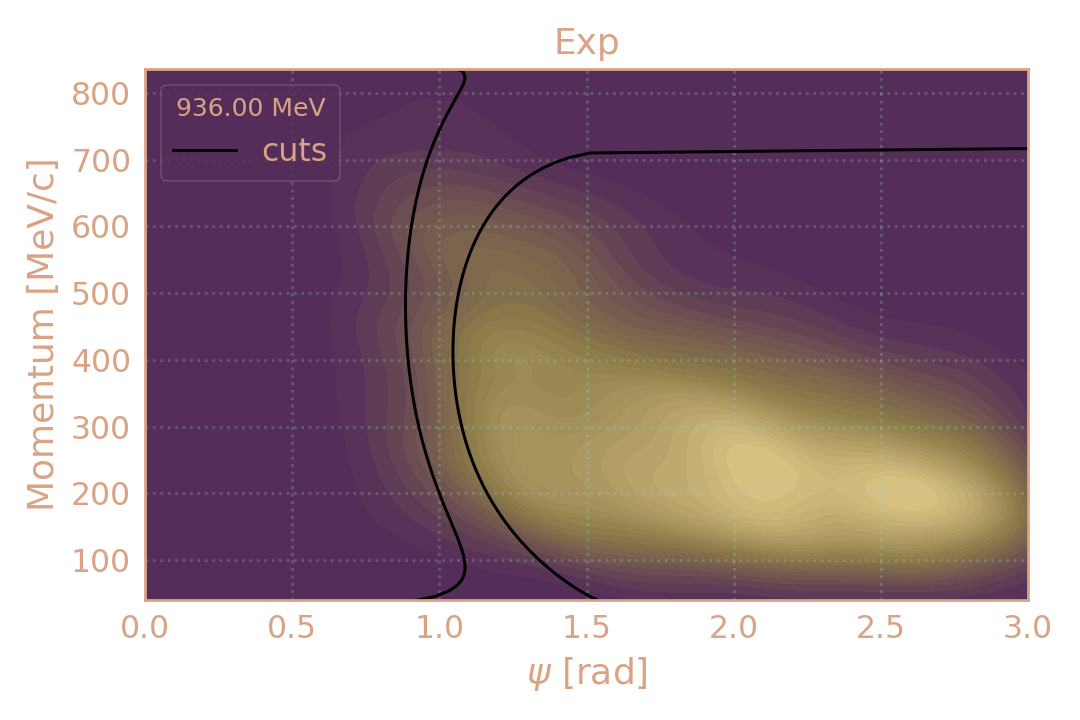
Распределение событий в эксп. (HIGH19, 936 MeV) по импульсу π± в зависимости от угла разлёта (ψ). Чёрным обозначены критерии отбора.
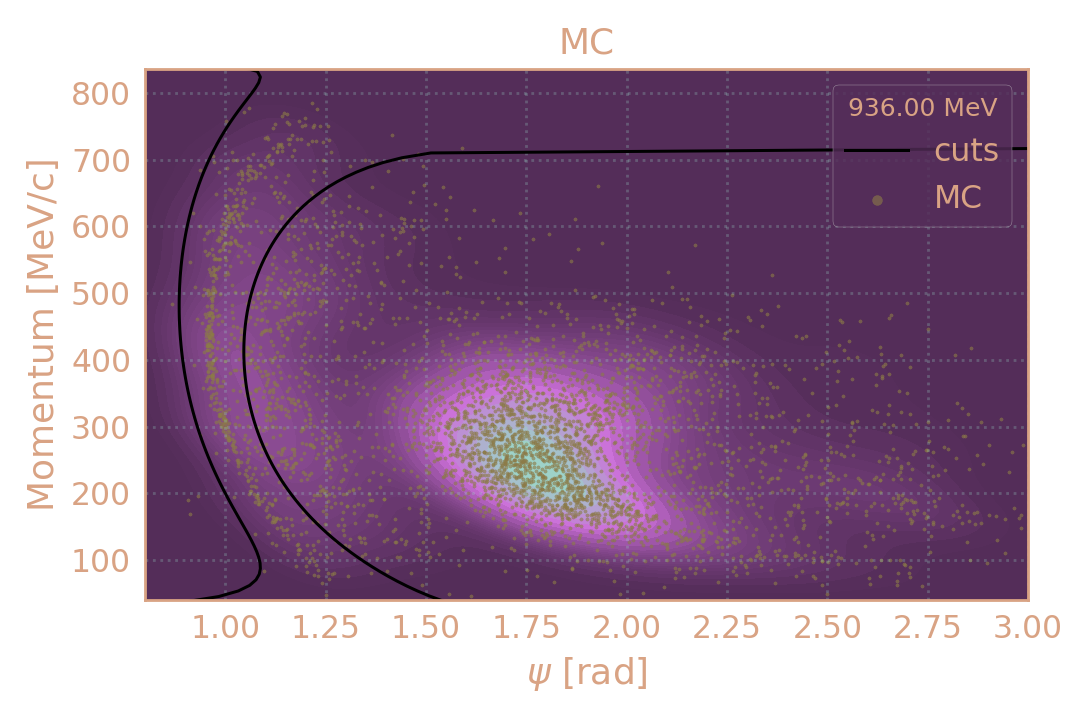
Распределение событий в MC (HIGH19, 936 MeV) по импульсу π± в зависимости от угла разлёта (ψ). Чёрным обозначены критерии отбора.
Критерии отбора событий
Для отобранных событий строю распределение по инв. массе KS в зависимости от импульса KS, а затем поворачиваю на "угол корреляции".
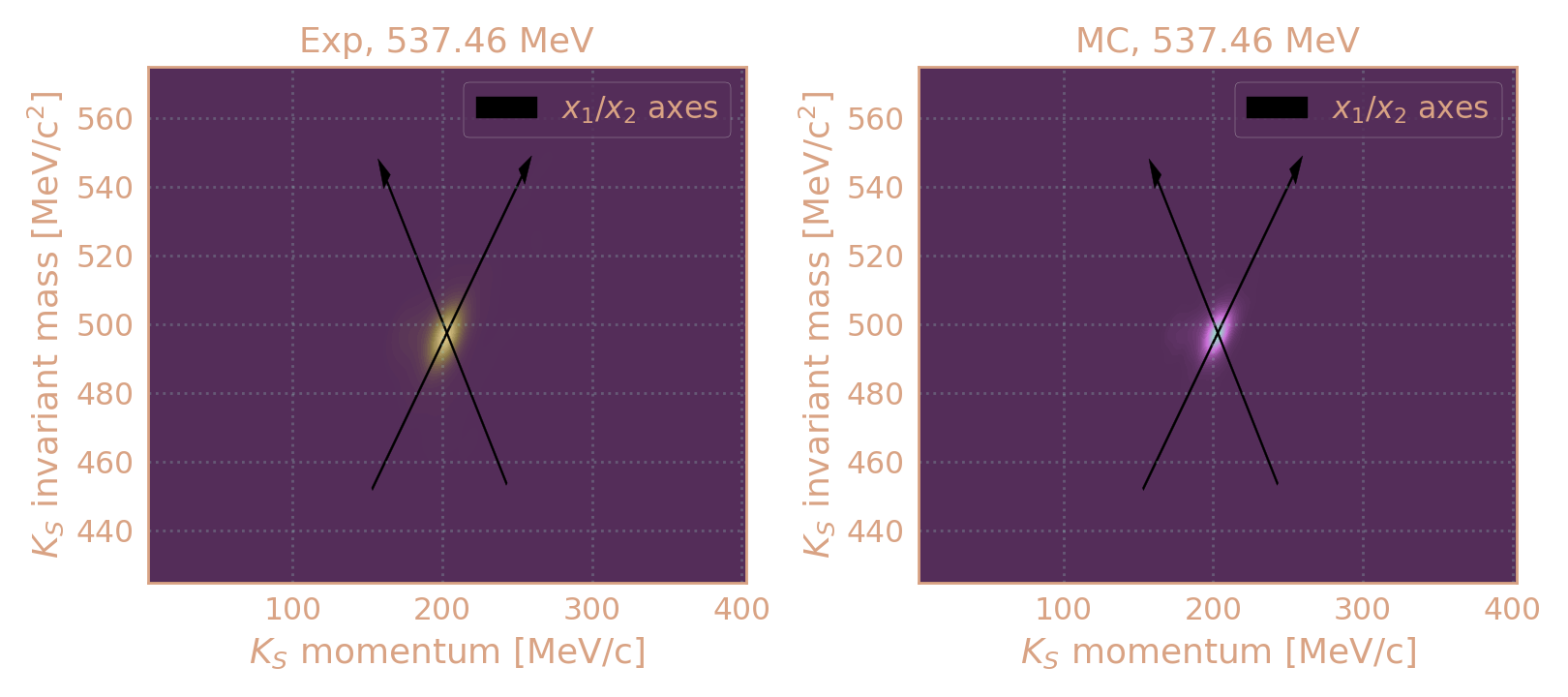
Распределение плотности событий в эксп. и MC (HIGH19, 537.5 MeV) по инв. массе KS в зависимости от его импульса. Чёрным обозначены оси после поворота на "угол корреляции".
Критерии отбора событий
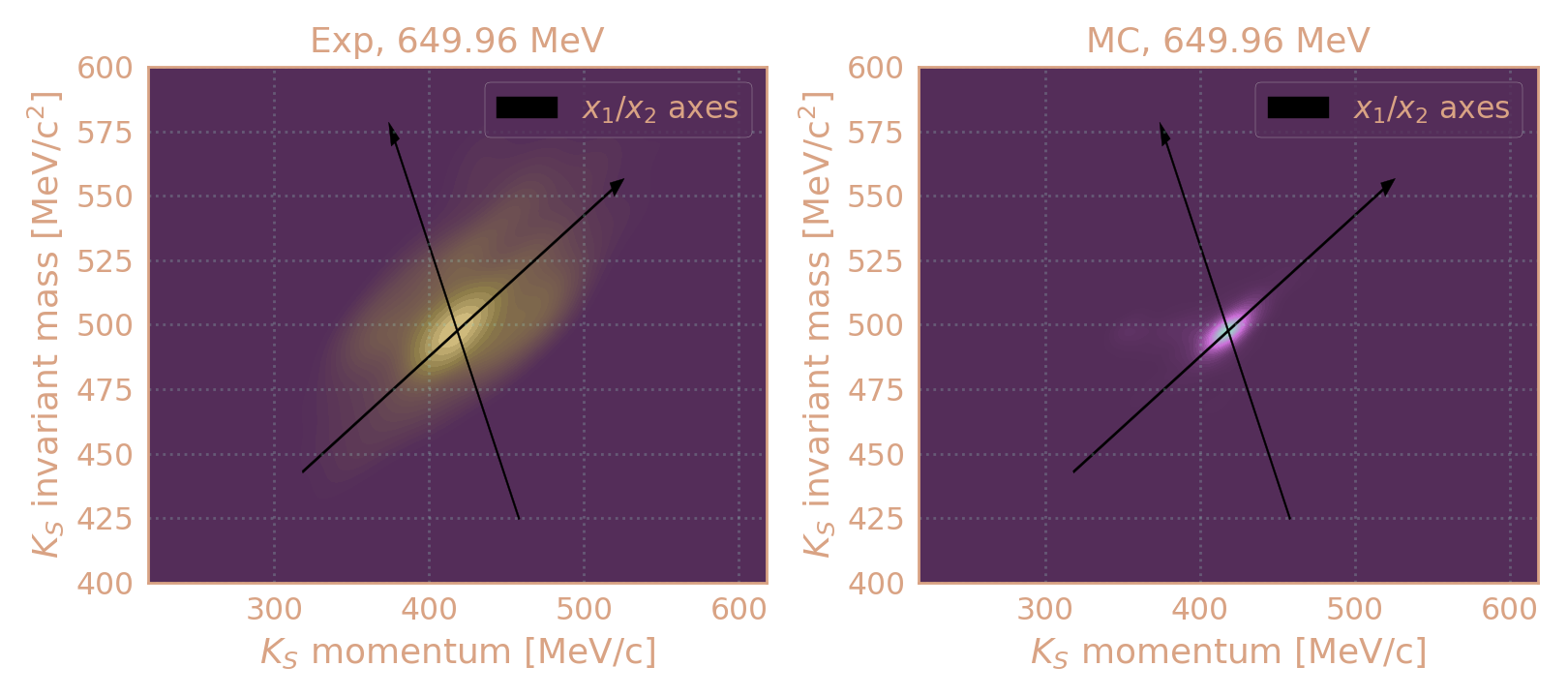
Распределение плотности событий в эксп. и MC (HIGH19, 650 MeV) по инв. массе KS в зависимости от его импульса. Чёрным обозначены оси после поворота на "угол корреляции".
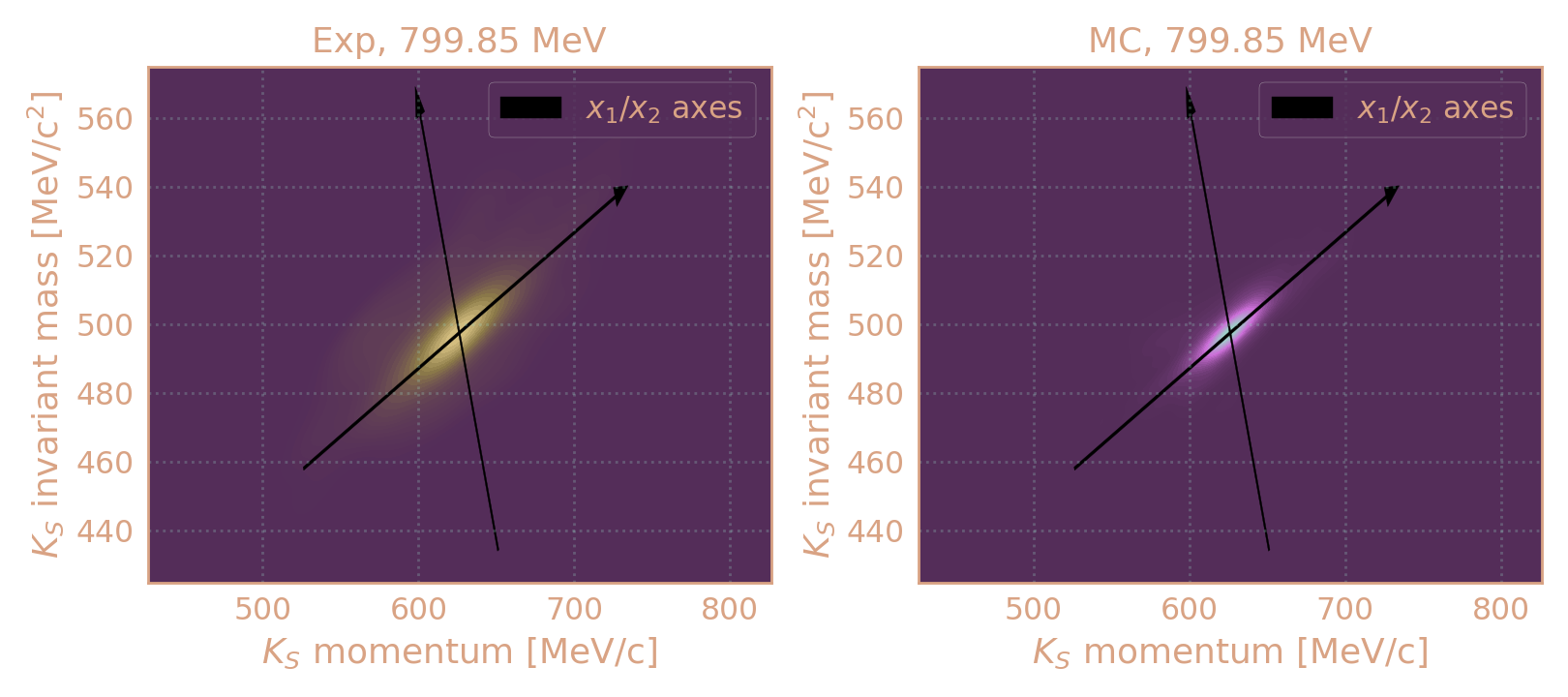
Распределение плотности событий в эксп. и MC (HIGH19, 800 MeV) по инв. массе KS в зависимости от его импульса. Чёрным обозначены оси после поворота на "угол корреляции".
Критерии отбора событий
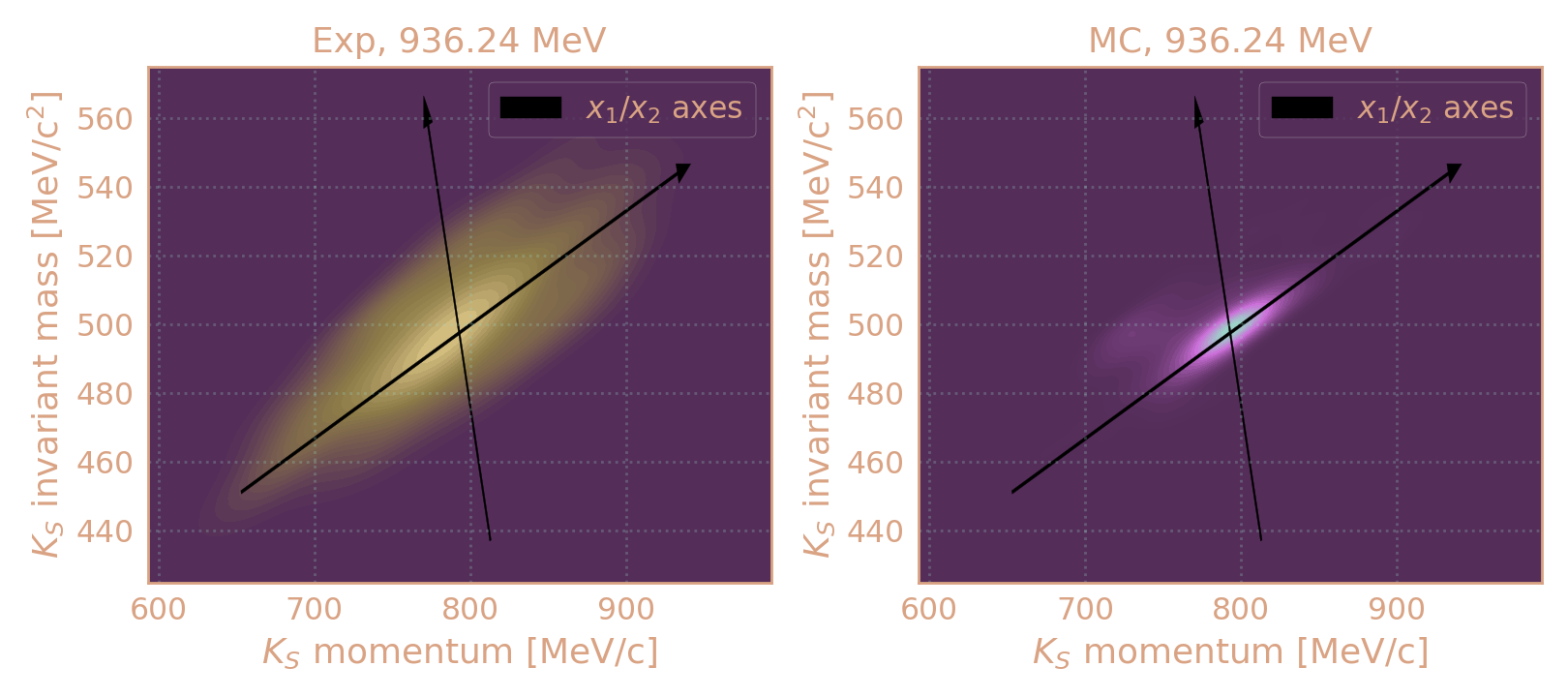
Распределение плотности событий в эксп. и MC (HIGH19, 936 MeV) по инв. массе KS в зависимости от его импульса. Чёрным обозначены оси после поворота на "угол корреляции".
Критерии отбора событий
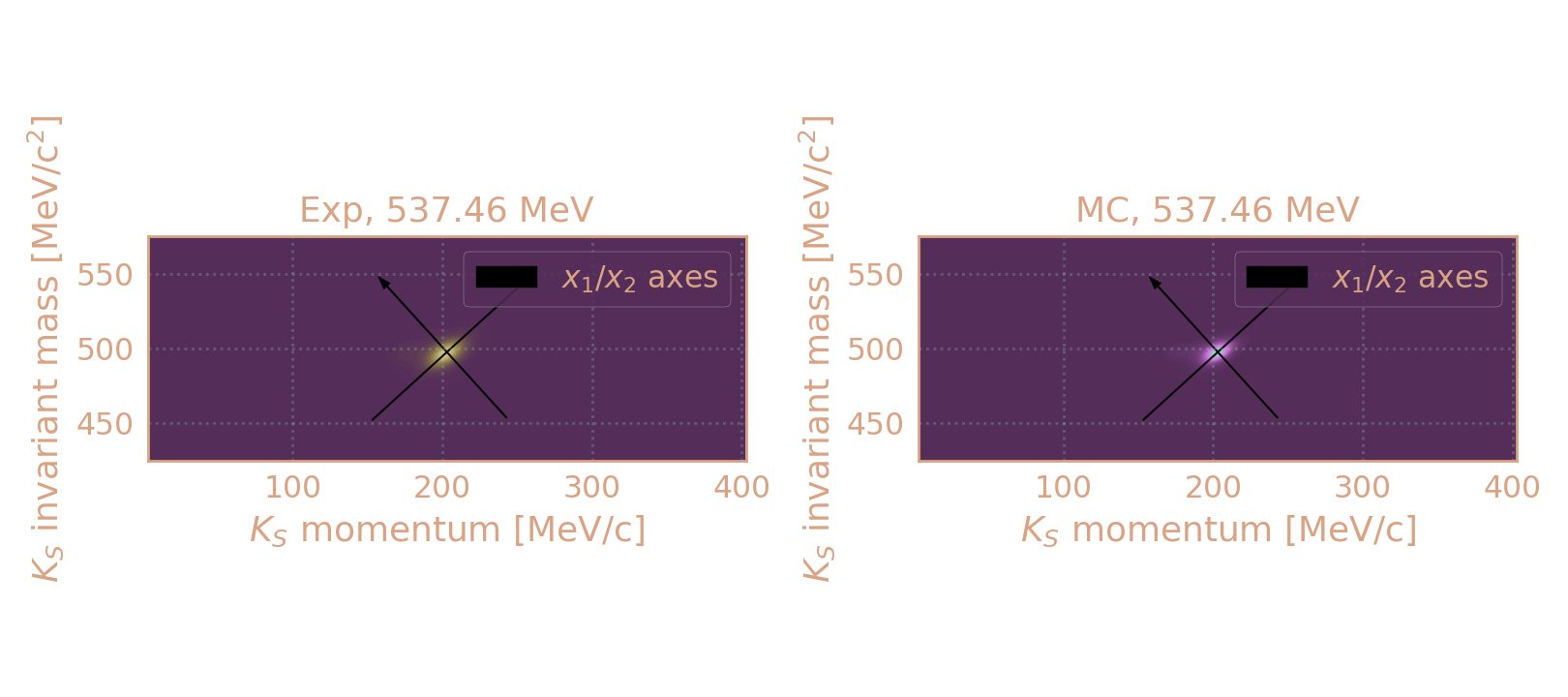
Распределение плотности событий в эксп. и MC (HIGH19, 537.5 MeV) по инв. массе KS в зависимости от его импульса с сохранением пропрорций. Чёрным обозначены оси после поворота на "угол корреляции".
Критерии отбора событий
С помощью MC Toy показываю, что между вычисленной инв. массой и импульсом может быть корреляция:
$$M_K^2 = 2 M_{\pi}^2 + 2 ( \epsilon_+ \epsilon_- - p_+ p_- \cos\psi ) $$
$$p_K^2 = p_+^2 + p_-^2 + 2 p_+ p_- \cos\psi $$
В реальности $$\psi = \psi^0 + \delta\psi$$ $$p_\pm = p_\pm^0 + \delta p_\pm$$
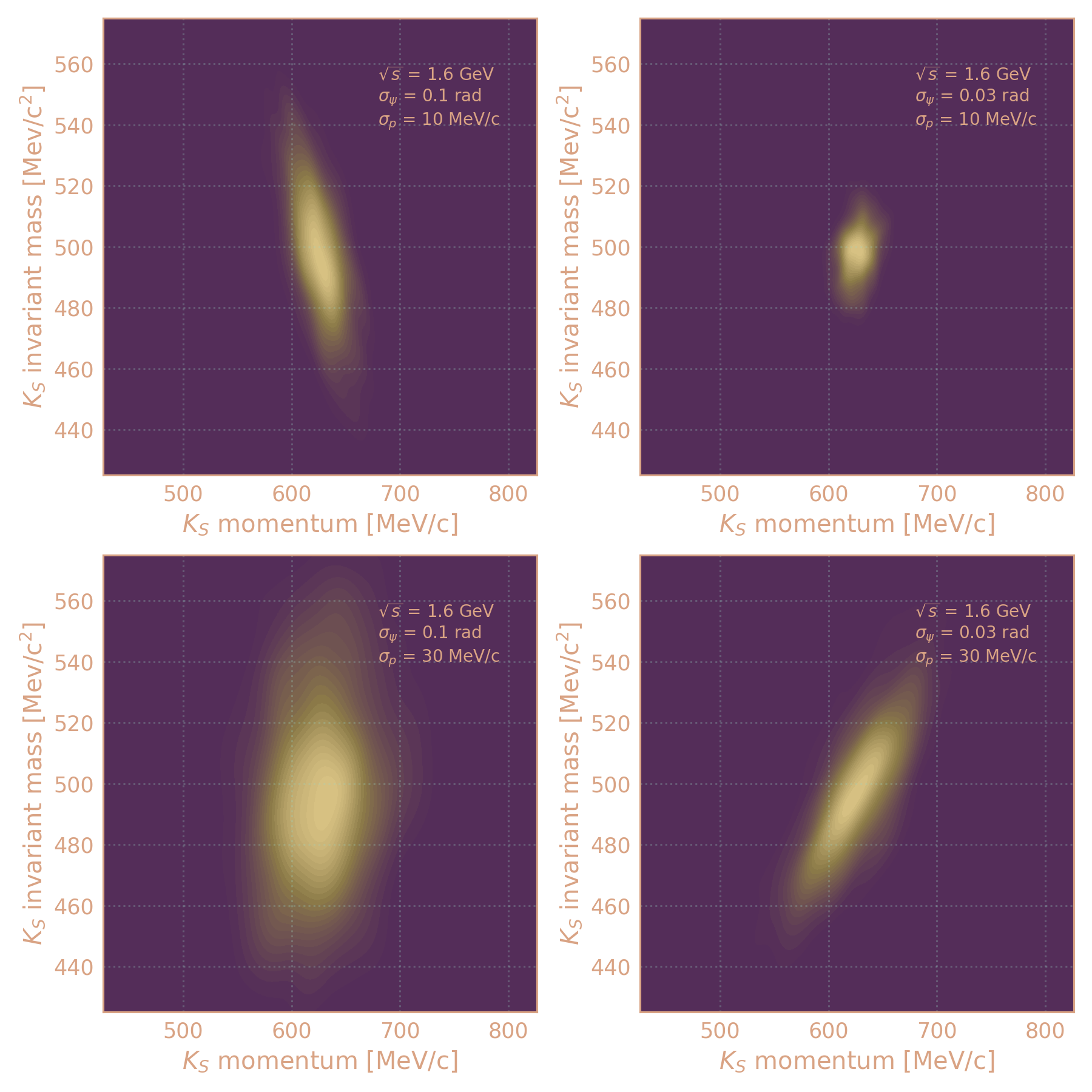
Определение числа событий
Распределения событий по x1 аппроксимировал функцией: \[f \sim N_{sig} \cdot \text{cruijff}(x, m, sL, sR, aL, aR) + N_{bkg} \cdot \text{poly2}(x, b, c)\]
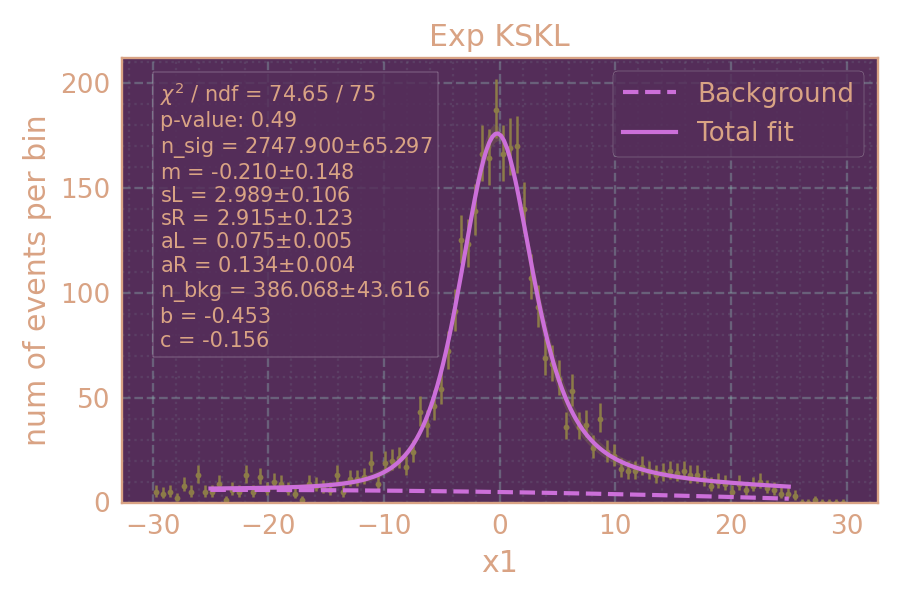
Распределение событий в эксп. (HIGH19, 537.5 MeV) по x1. Показана аппроксимация сигнал + фон (сплошная лин.) и отдельно фон (пунктирн.)
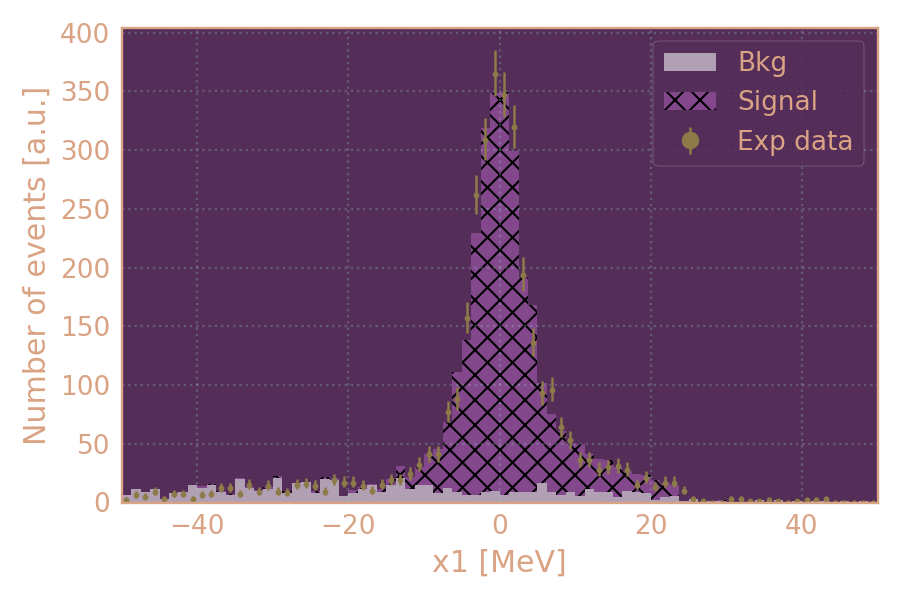
Распределение событий в эксп. (HIGH19, 537.5 MeV) по x1. Показан вклад сигнала (согласно MCGPJ MC) и фона (multihadrons gen)
Определение числа событий
Функция аппроксимации:
\[ \text{cruijff}(x, m, s_L, s_R, a_L, a_R) \sim \begin{cases} \exp{\big(\frac{(x-m)^2}{2( s_L^2 + a_L (x-m)^2)}\big)}, x < m\\ \exp{\big(\frac{(x-m)^2}{2( s_R^2 + a_R (x-m)^2)}\big)}, x \geq m \end{cases} \]
\[ \text{poly2}(x, b, c) \sim 1 + b \cdot x + c \cdot (3x^2 -1)/2 \]
Определение числа событий
Аппроксимация MC для HIGH19, 537.5 MeV
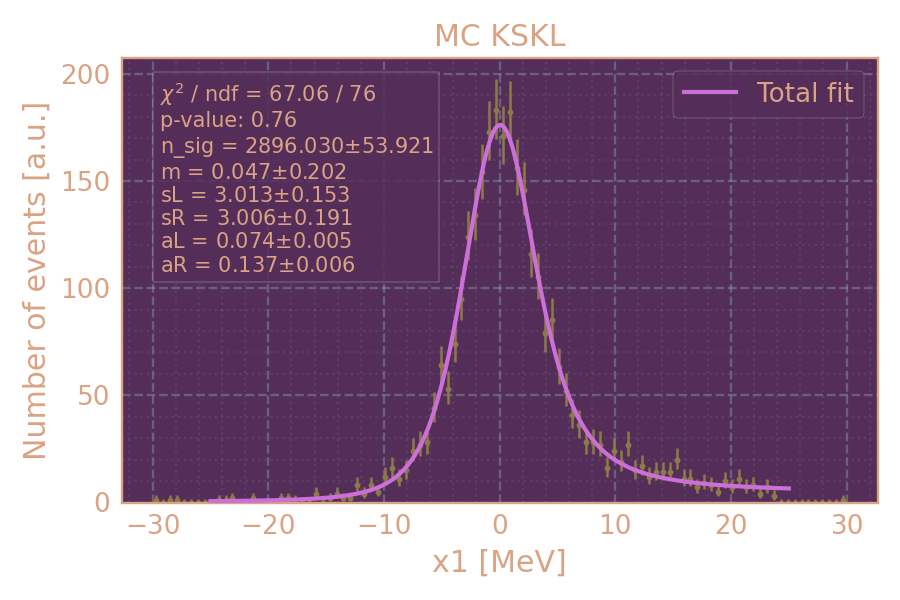
Распределение событий в MC KSKL (HIGH19, 537.5 MeV, MCGPJ) по x1 и аппроксимация.
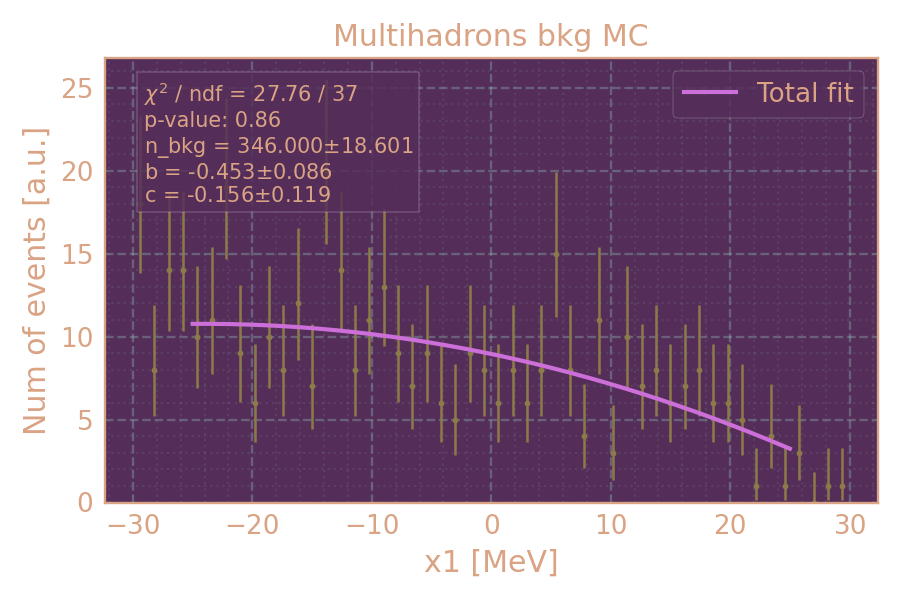
Распределение событий в MC фон (HIGH19, 537.5 MeV, multihadrons) по x1 и аппроксимация.
Определение числа событий
Аппроксимация exp для HIGH19, 537.5 MeV

Распределение событий в эксперименте (HIGH19, 537.5 MeV, MCGPJ) по x1 и аппроксимация. Сигнал + фон — сплошная линия; фон — пунктирная линия.

Распределение событий в эксперименте (HIGH19, 537.5 MeV, MCGPJ) по x1. Показан вклад сигнала (согласно MCGPJ MC KSKL) и фона (multihadrons gen).
Определение числа событий
Аппроксимация MC для HIGH19, 650 MeV
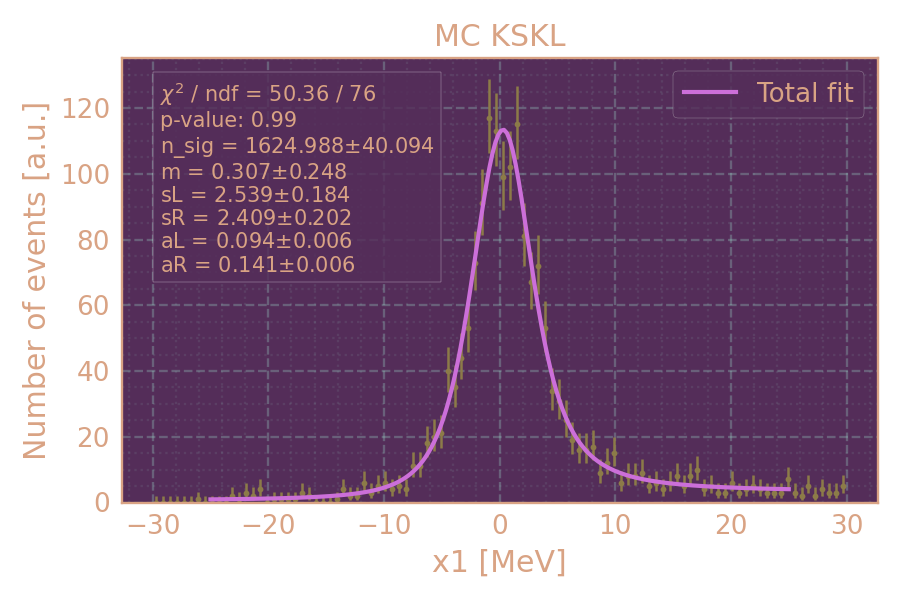
Распределение событий в MC KSKL (HIGH19, 650 MeV, MCGPJ) по x1 и аппроксимация.
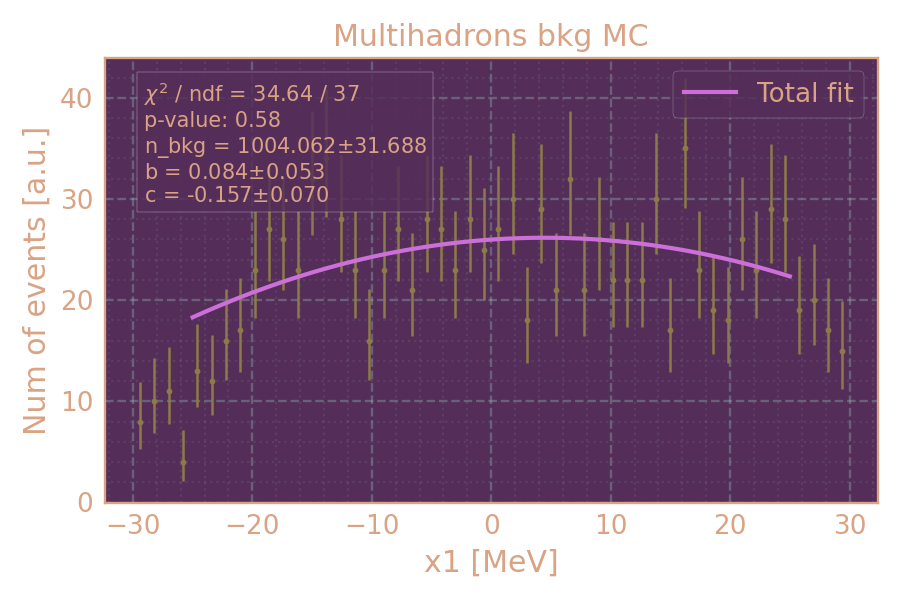
Распределение событий в MC фон (HIGH19, 650 MeV, multihadrons) по x1 и аппроксимация.
Определение числа событий
Аппроксимация exp для HIGH19, 650 MeV
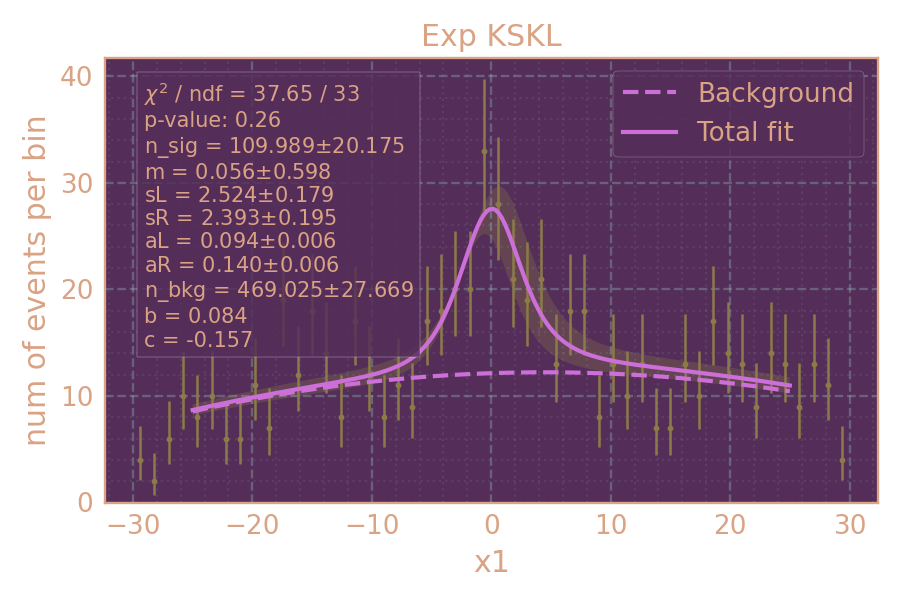
Распределение событий в эксперименте (HIGH19, 650 MeV, MCGPJ) по x1 и аппроксимация. Сигнал + фон — сплошная линия; фон — пунктирная линия.
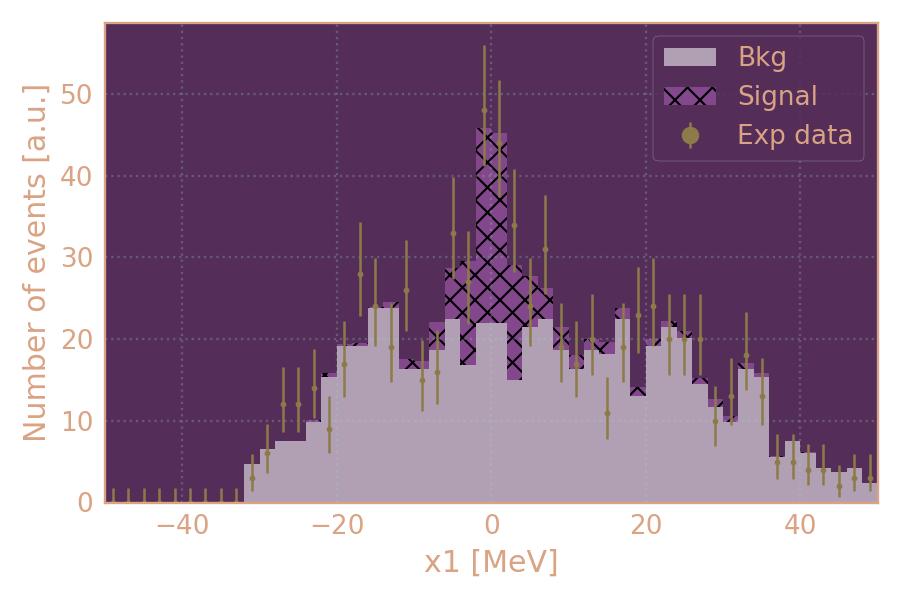
Распределение событий в эксперименте (HIGH19, 650 MeV, MCGPJ) по x1. Показан вклад сигнала (согласно MCGPJ MC KSKL) и фона (multihadrons gen).
Определение числа событий
Аппроксимация MC для HIGH19, 800 MeV
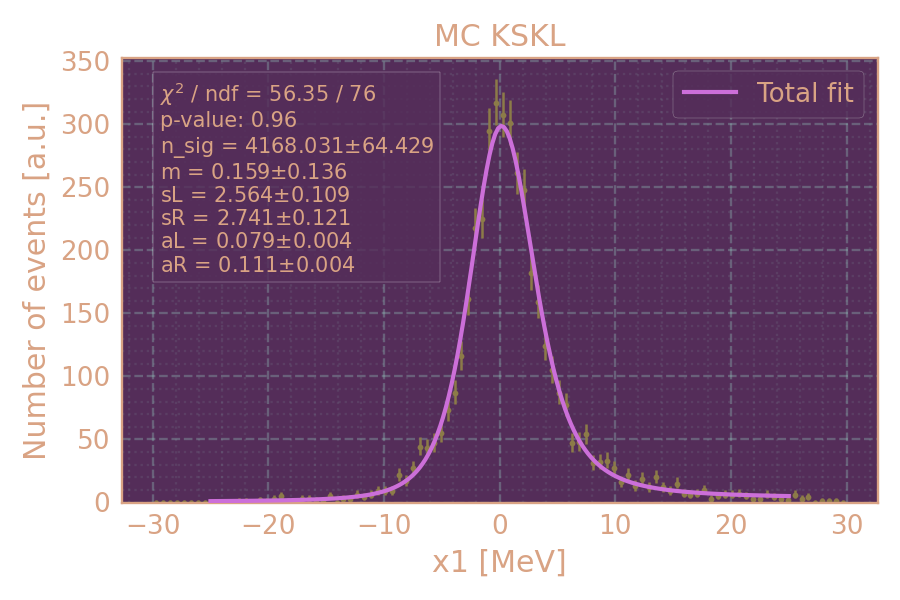
Распределение событий в MC KSKL (HIGH19, 800 MeV, MCGPJ) по x1 и аппроксимация.
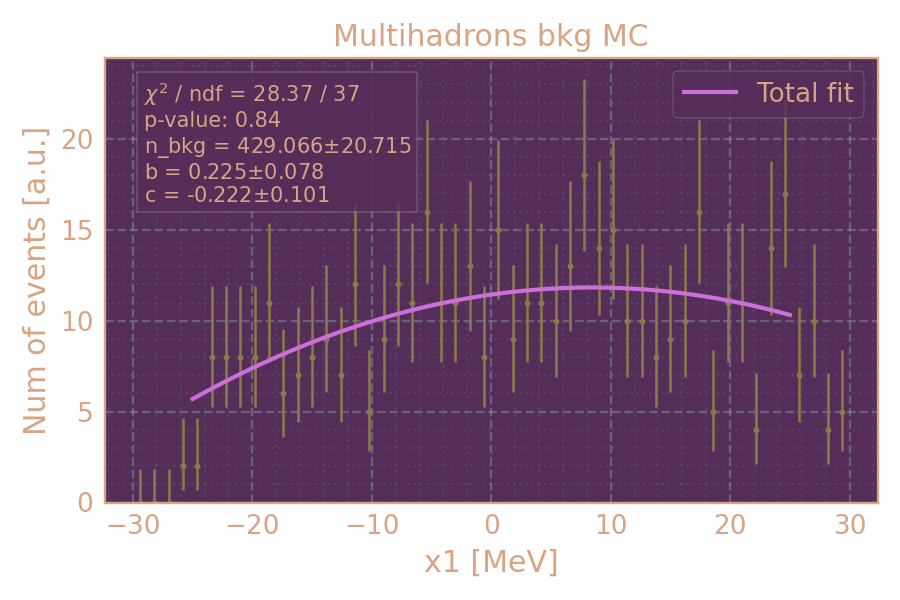
Распределение событий в MC фон (HIGH19, 800 MeV, multihadrons) по x1 и аппроксимация.
Определение числа событий
Аппроксимация exp для HIGH19, 800 MeV
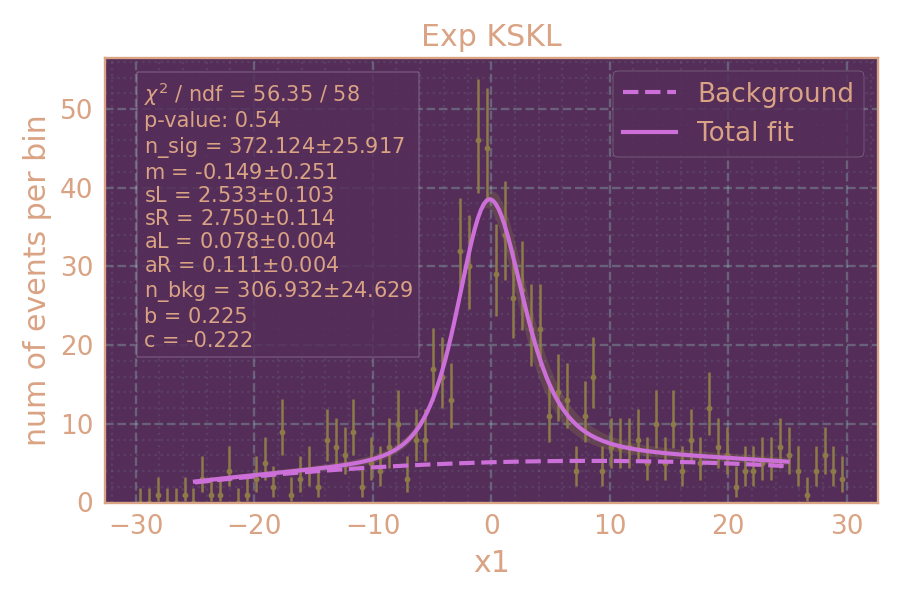
Распределение событий в эксперименте (HIGH19, 800 MeV, MCGPJ) по x1 и аппроксимация. Сигнал + фон — сплошная линия; фон — пунктирная линия.
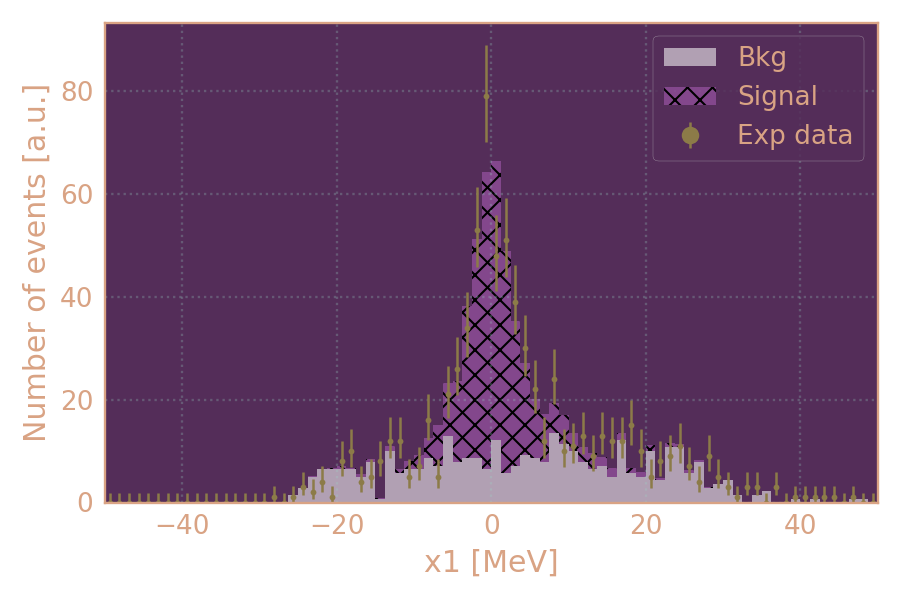
Распределение событий в эксперименте (HIGH19, 800 MeV, MCGPJ) по x1. Показан вклад сигнала (согласно MCGPJ MC KSKL) и фона (multihadrons gen).
Определение числа событий
Аппроксимация MC для HIGH19, 936 MeV
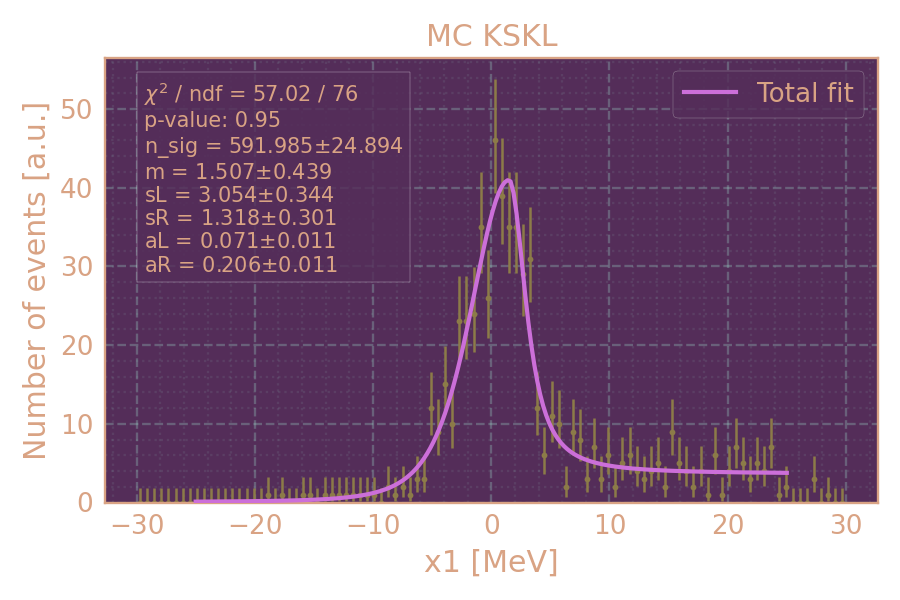
Распределение событий в MC KSKL (HIGH19, 936 MeV, MCGPJ) по x1 и аппроксимация.
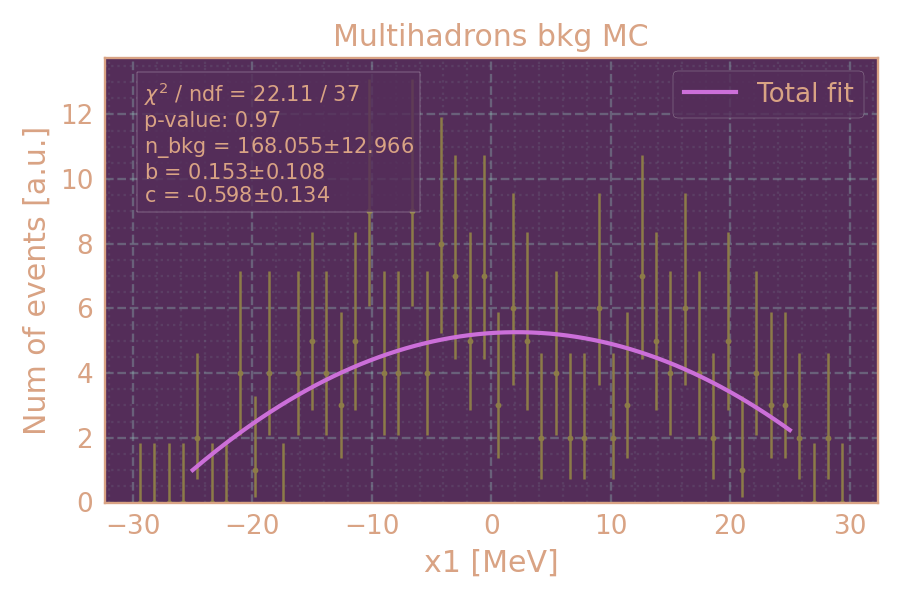
Распределение событий в MC фон (HIGH19, 936 MeV, multihadrons) по x1 и аппроксимация.
Определение числа событий
Аппроксимация exp для HIGH19, 936 MeV
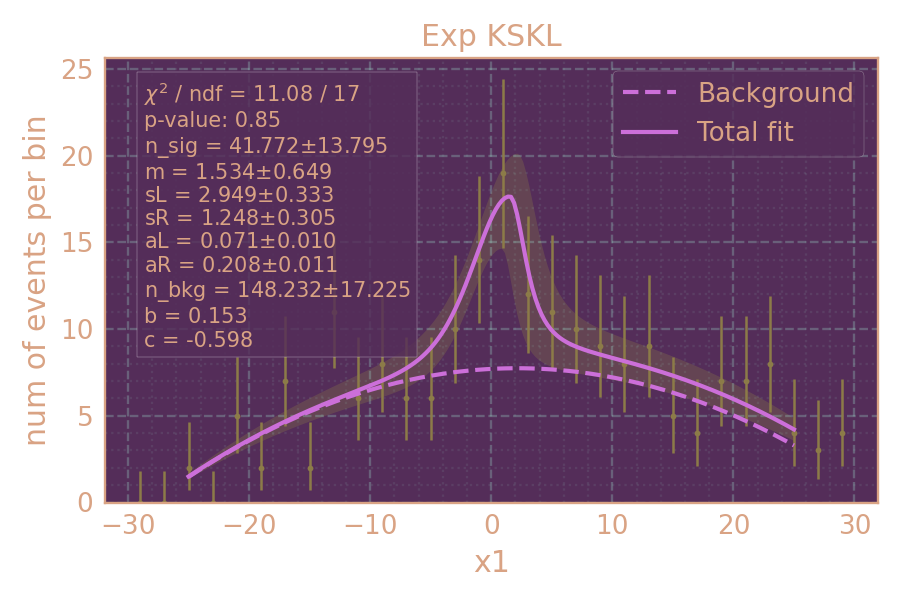
Распределение событий в эксперименте (HIGH19, 936 MeV, MCGPJ) по x1 и аппроксимация. Сигнал + фон — сплошная линия; фон — пунктирная линия.
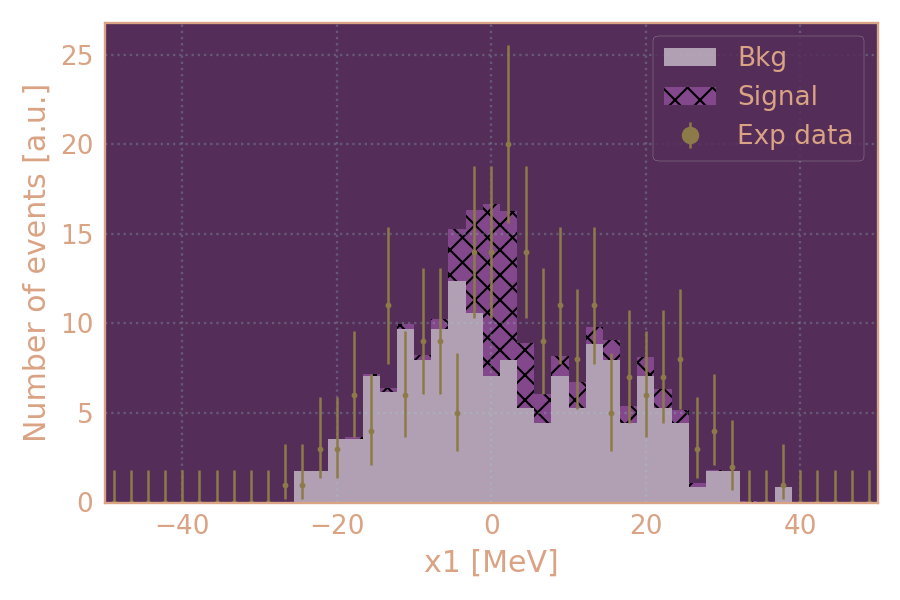
Распределение событий в эксперименте (HIGH19, 936 MeV, MCGPJ) по x1. Показан вклад сигнала (согласно MCGPJ MC KSKL) и фона (multihadrons gen).
Структура фона (multihadrons gen)
| Ebeam [МэВ] | Основные фон. процессы |
|---|---|
| 537.5 | 2π±2π0 (70%), π+π-π0 (19%), π+π- (7%), |
| 650 | 2π±2π0 (89%), π+π-π0 (7%), |
| 800 | 2π±2π0 (86%), π+π-η (9%) |
| 936 | 2π±2π0 (82%), π+π-η (10%), π+π-3π0 (3%) |
Эффективность триггеров
\[ \varepsilon_{trig} = 1 - (1- \varepsilon_{TF}) (1 - \varepsilon_{CF}) \]
\[ \varepsilon_{TF} = \frac{N_{TF\&CF} + 1}{N_{CF} + N_{TF\&CF} + 2} \]
\[ \varepsilon_{CF} = \frac{N_{TF\&CF} + 1}{N_{TF} + N_{TF\&CF} + 2} \]
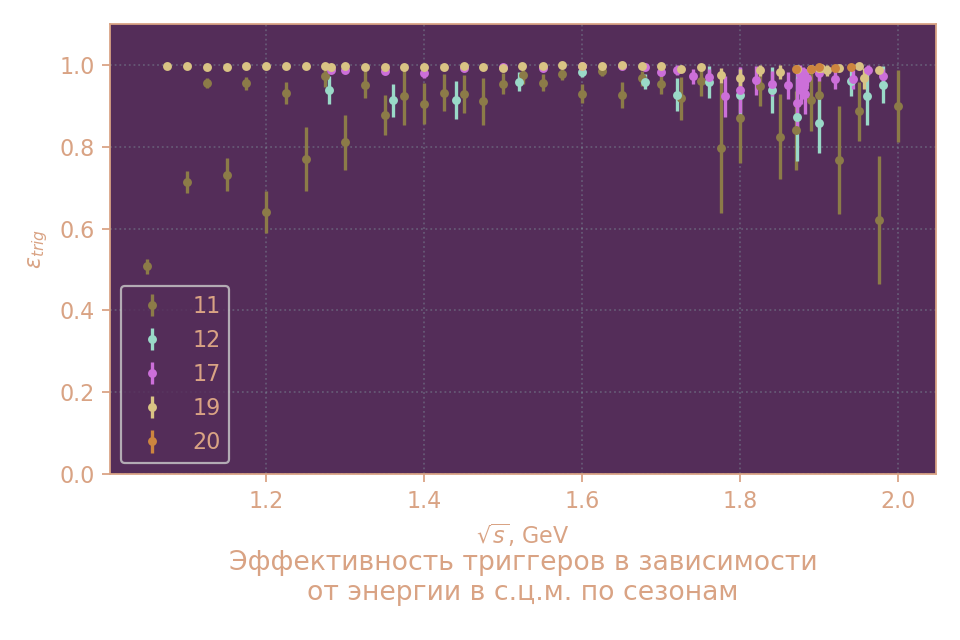
Эффективность регистрации
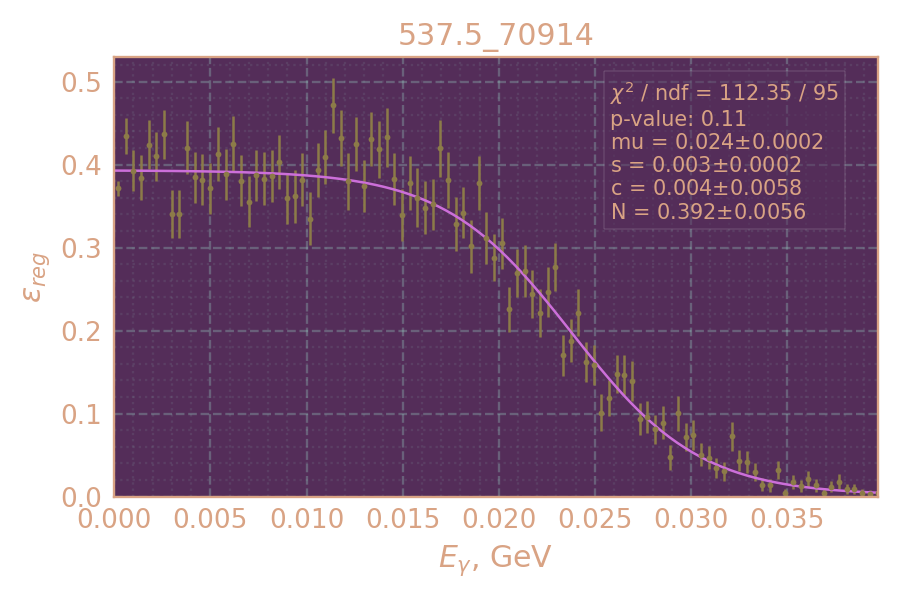
Определяю и аппроксимирую эффективность регистрации в зависимости от энергии радиационного фотона (использую MC KSKL с равномерно распр. рад. фотоном)
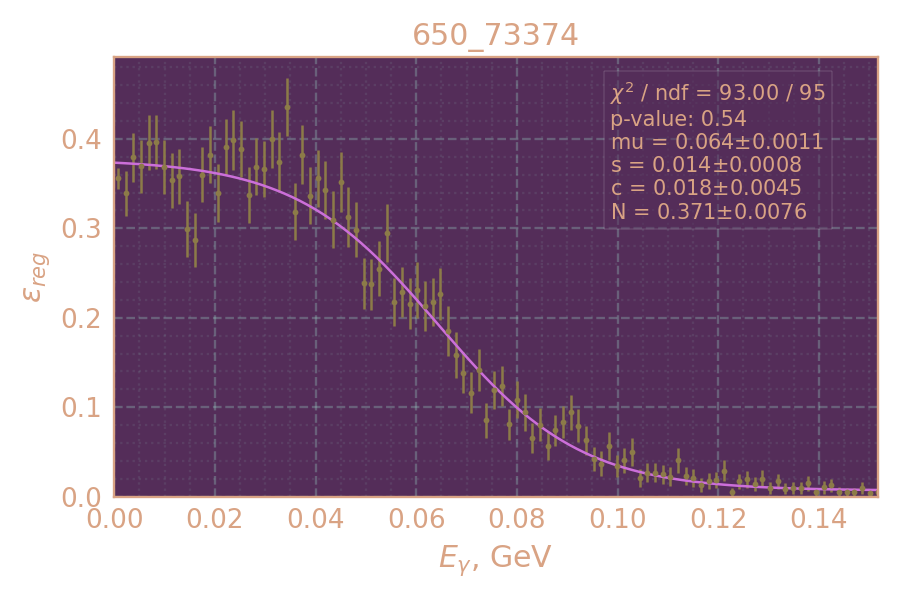
Эффективность регистрации
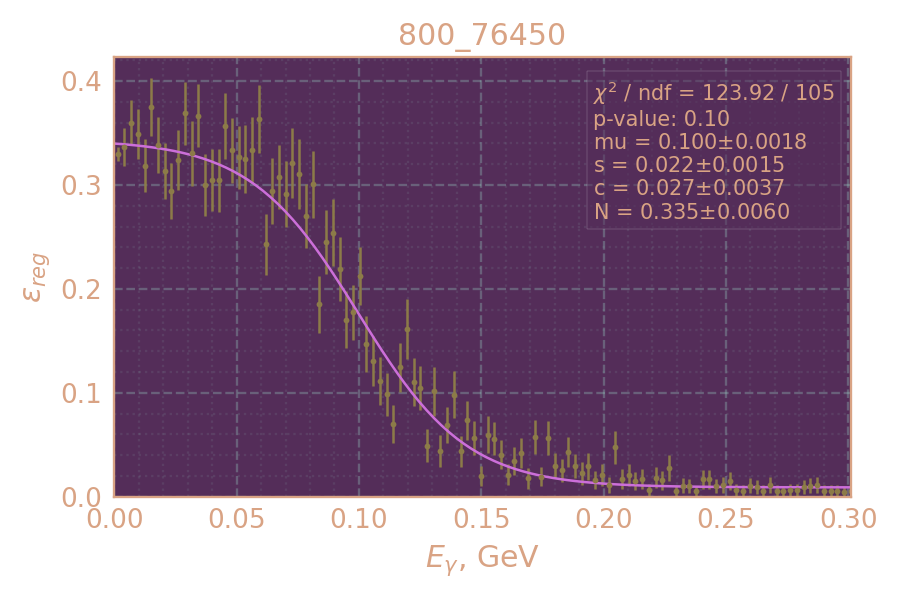
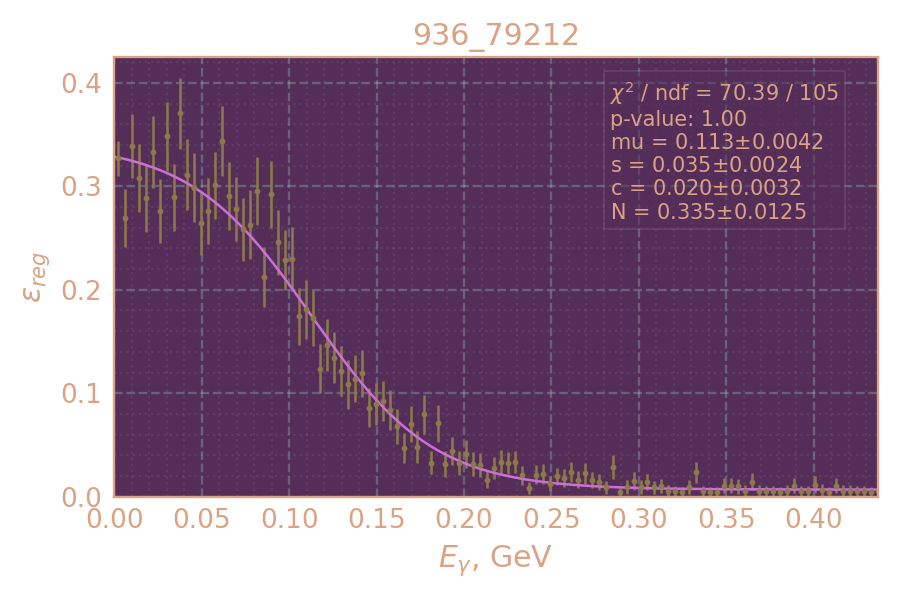
Определяю и аппроксимирую эффективность регистрации в зависимости от энергии радиационного фотона (использую MC KSKL с равномерно распр. рад. фотоном)
Рад. поправки
Радиационная поправка определяется по формуле: \[ \sigma_{vis} = \int_0^1 F(x, s) \sigma_{born} (s [1-x]) \varepsilon_{reg}(x,s)dx = \sigma_{born} \varepsilon (1+\delta) \]
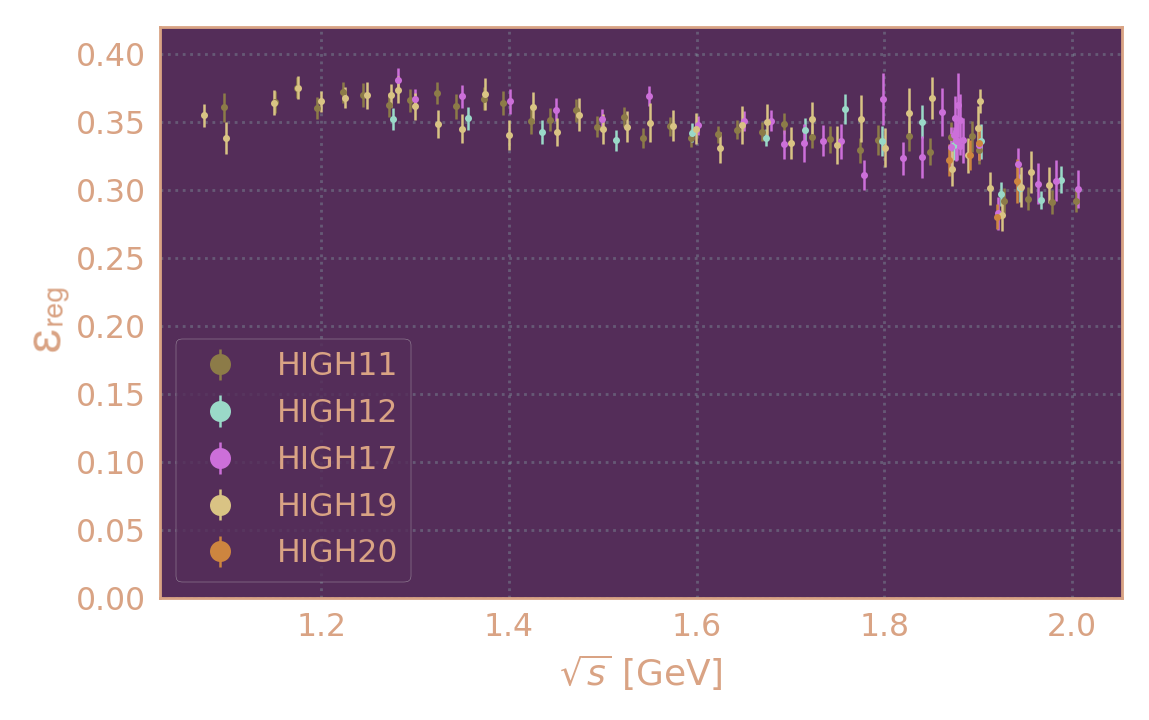
Эффективность регистрации для рад.фотона с нулевой энергией в зависимости от энергии в с.ц.м. по сезонам
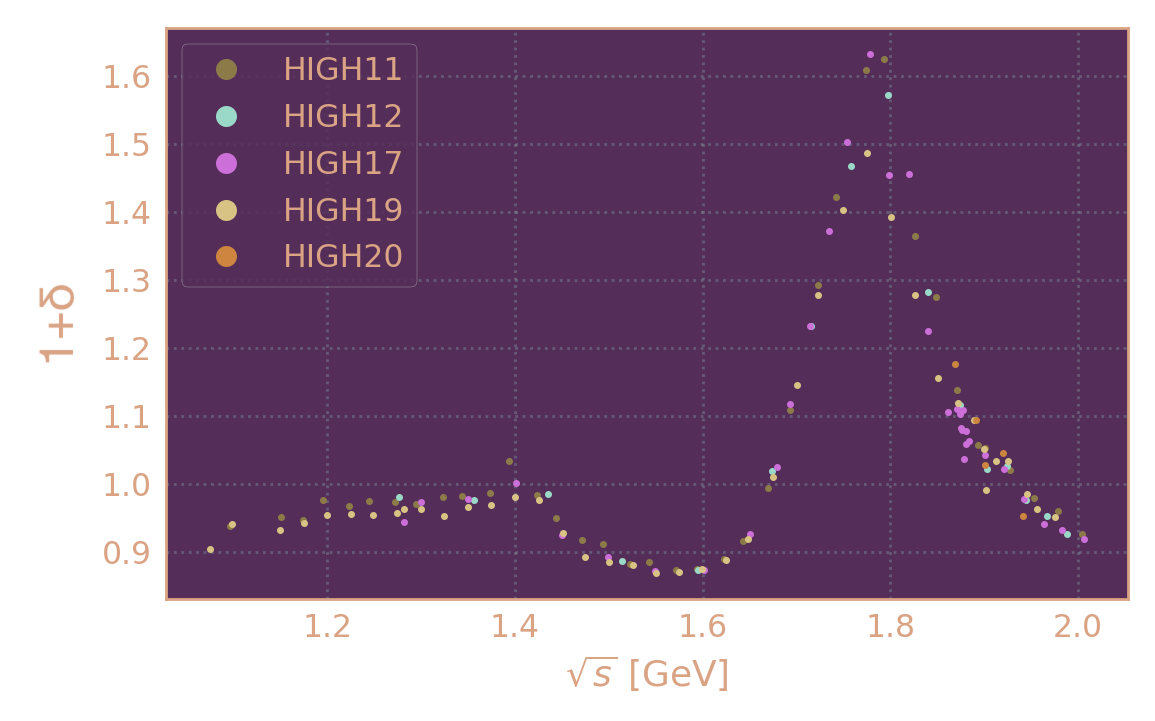
Рад.поправка в зависимости от энергии в с.ц.м. по сезонам
Поправка на эффективность ДК
Для определения поправки на эффективность ДК я отбирал события с одним треком, летящим ортогонально ДК (π/2 - 0.3 < θ < π/2 + 0.3) и сравнивал распределения второго трека по углам и импульсам в эксперименте и MC.
Поправка на эффективность ДК в зависимости от полярного угла в сезоне HIGH11
Поправка на эффективность ДК
Распределение событий по полярному углу второго трека в эксперименте и MC (HIGH11). Количество событий отнормировано на область между чёрными линиями.
Распределение событий по импульсу второго трека в эксперименте и MC (HIGH11).
Поправка на эффективность ДК
Распределение событий по полярному углу второго трека в эксперименте и MC (HIGH19). Количество событий отнормировано на область между чёрными линиями.
Поправка на эффективность ДК в зависимости от полярного угла в сезоне HIGH19.
Поправка на эффективность ДК
Распределение событий по полярному углу второго трека в эксперименте и MC (HIGH17). Количество событий отнормировано на область между чёрными линиями.
Поправка на эффективность ДК в зависимости от полярного угла в сезоне HIGH17.
Поправка на эффективность ДК
Распределение событий по полярному углу второго трека в эксперименте и MC (HIGH12). Количество событий отнормировано на область между чёрными линиями.
Поправка на эффективность ДК в зависимости от полярного угла в сезоне HIGH12.
Поправка на эффективность ДК
Распределение событий по полярному углу второго трека в эксперименте и MC (HIGH20). Количество событий отнормировано на область между чёрными линиями.
Поправка на эффективность ДК в зависимости от полярного угла в сезоне HIGH20.
Сечение процесса
\[ \sigma_{born} = \frac{N_{sig}}{\varepsilon L (1 + \delta)} \]
Зависимость сечения процесса e+e– ➝ KSKL от энергии в с.ц.м. по сезонам в логарифмическом масштабе (без учёта поправок на ДК).
Сечение процесса
Зависимость сечения процесса e+e– ➝ KSKL от энергии в с.ц.м. по сезонам в логарифмическом масштабе.
Зависимость сечения процесса e+e– ➝ KSKL от энергии в с.ц.м. по сезонам в symlog масштабе.
Систематические ошибки
- Сдвигать каты (как быть с катом P-ψ?)
- Какие ещё методы (лайклихуд)?
- Что нужно проверить?
Систематические ошибки
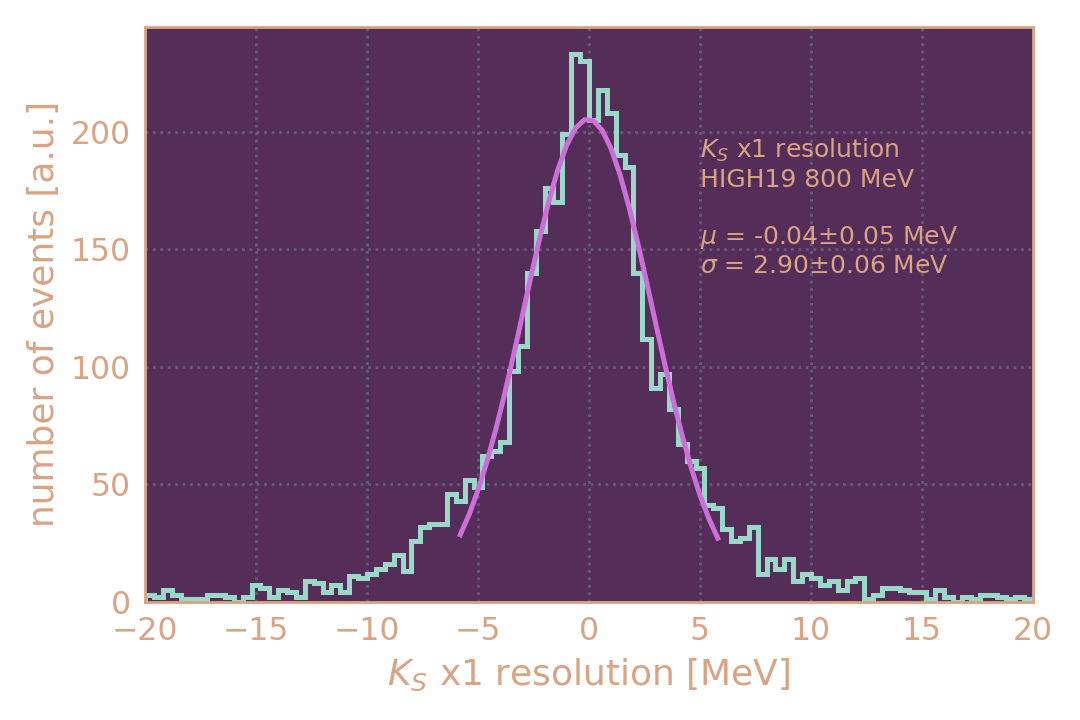
Распределение событий в MC KSKL по разнице между генерированным и восстановленным параметром x1 (разрешение по x1).
| Ebeam [МэВ] | Сист. ошибка от x1 (%) | Стат. ошибка (%) |
|---|---|---|
| 537.5 | 0.3 | 2.5 |
| 650 | 1.6 | 18 |
| 800 | 0.2 | 7 |
| 936 | 6 | 36 |
Будущие планы
- Проверить поправку на эффективность ДК
- Совместный анализ с e+e– ➝ K+K–
- Определить систематические ошибки
- Представить результаты работы на конференциях и т.д.