Изучение процесса e+e– ➝ KSKL
в диапазоне энергий 1.05 – 2.0 ГэВ
в с.ц.м. с детектором КМД-3
Никита Петров, 2 к. асп. ФФ НГУ
Научный руководитель: Лукин П.А.
Цель работы
Измерить сечение процесса e+e– ➝ KSKL в диапазоне энергий 1.05 – 2.0 ГэВ в с.ц.м.
Детектор КМД-3 и коллайдер ВЭПП-2000
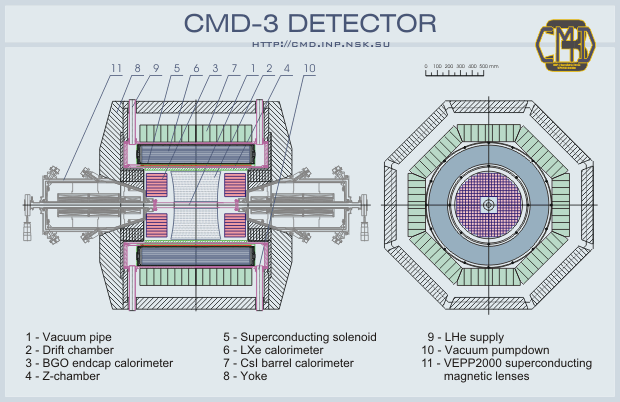
Детектор КМД-3
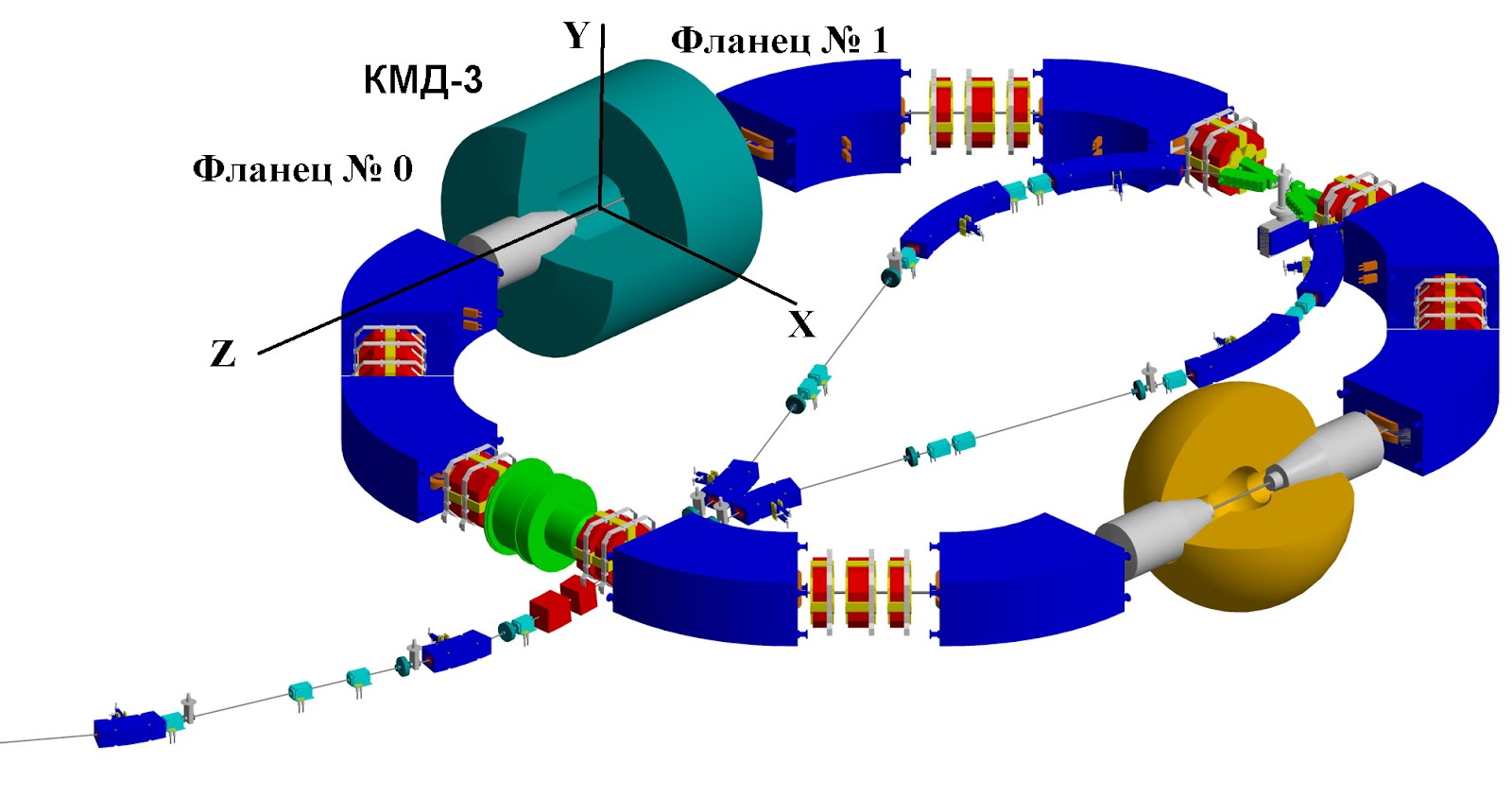
ВЭПП-2000
План презентации
- Анализ процесса e+e– ➝ KSKL
- Критерии отбора событий
- Поправка к эффективности реконструкции треков в ДК
- Эффективность триггеров
- Эффективность регистрации
- Радиационные поправки
- Сечение процесса
- Систематические ошибки
- Обсуждение результатов и перспективы
КМУ 2020
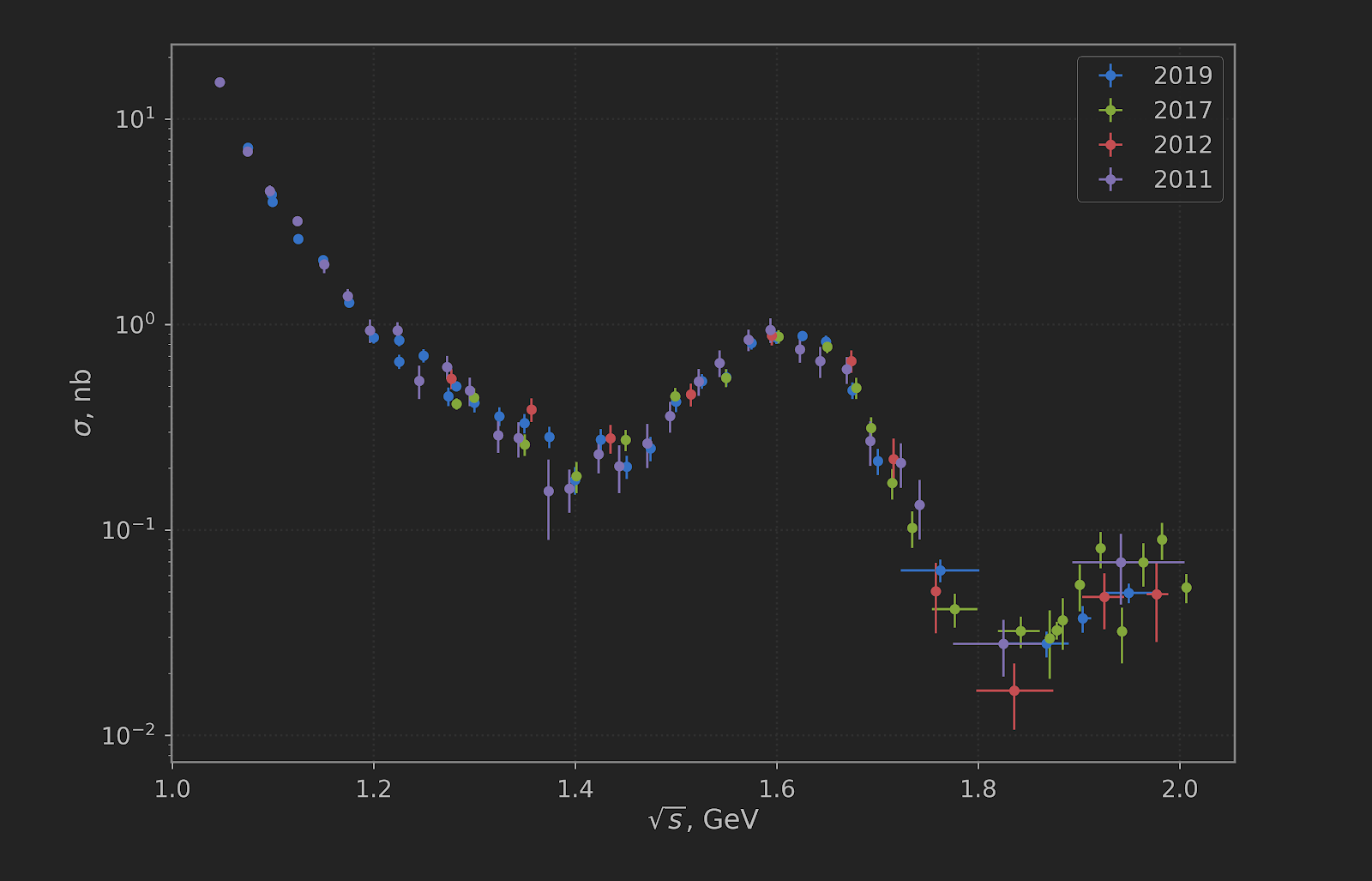
Сечение процесса e+e– ➝ KSKL, продемонстрированное на КМУ 2020
Проблема ρ
Отбор по прицельному параметру |ρ| > 0,1 см эффективно устраняет фон, но даёт вклад в систематику до 5%.
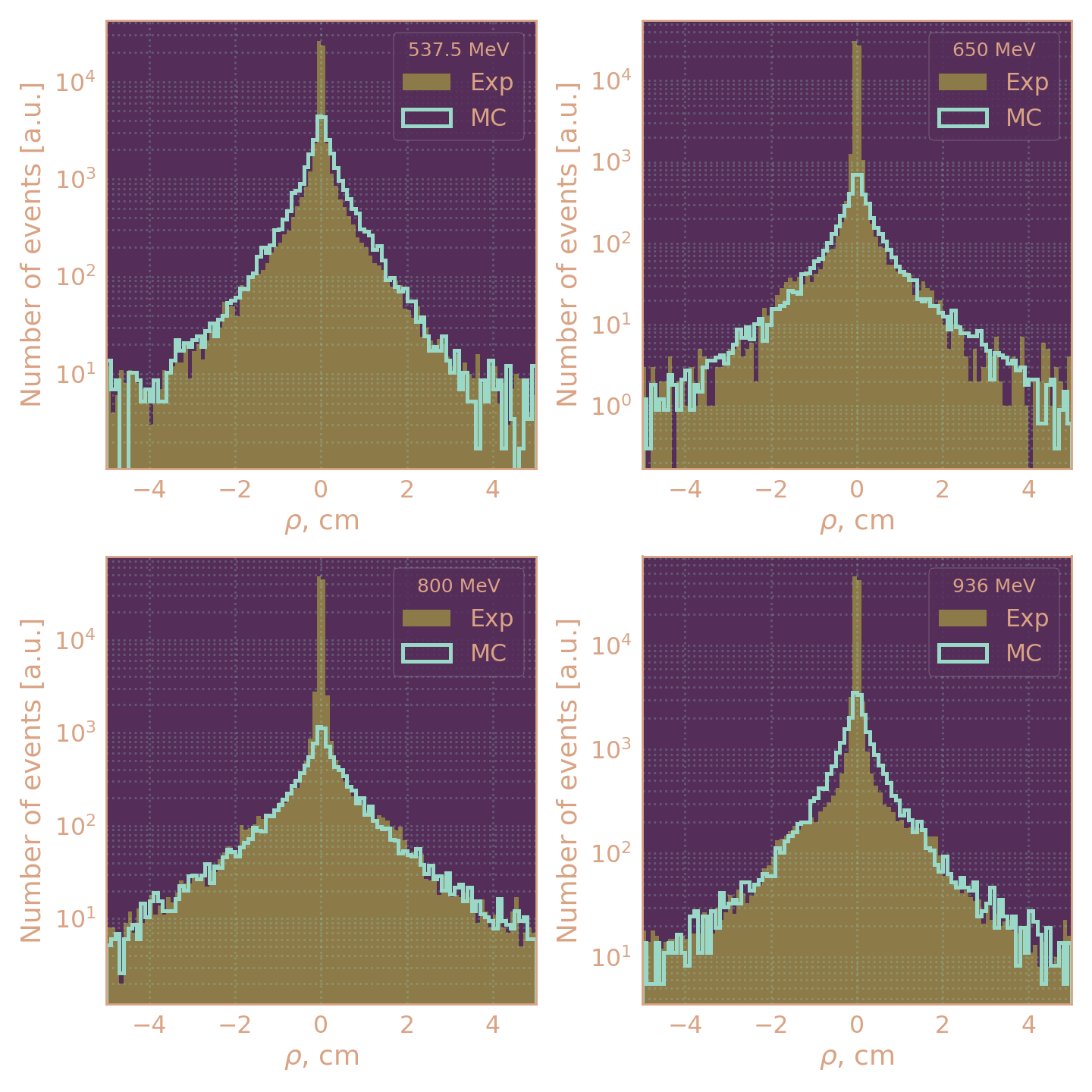
Распределения событий в эксперименте и МС сигнального процесса по ρ (нормировано на
Проблема ρ
Влияние отбора по ρ на распределения по параметру аппроксимации x1.
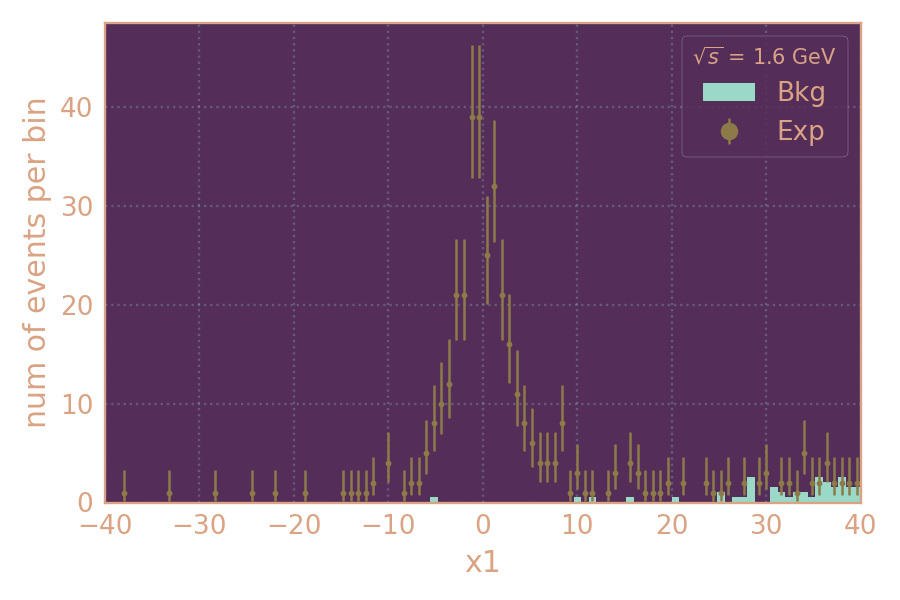
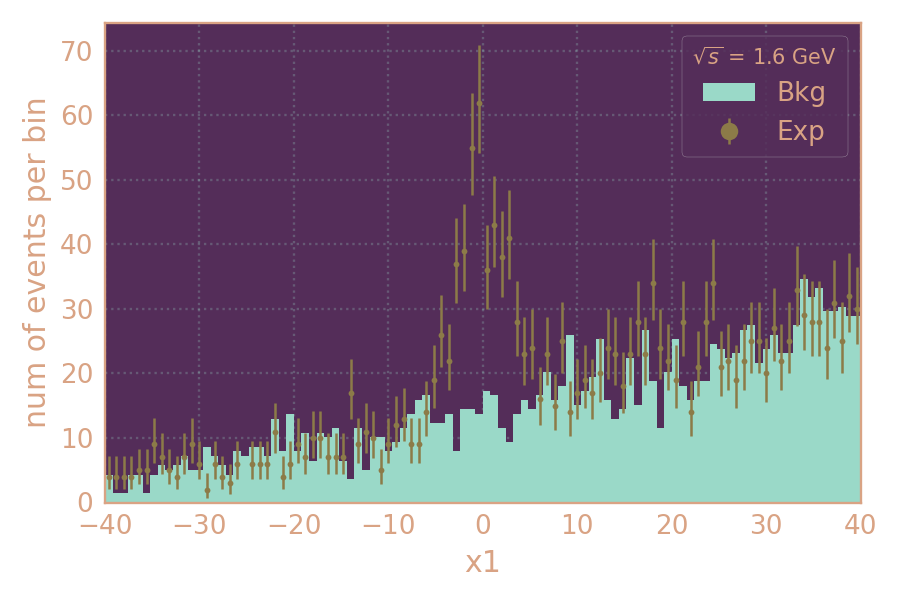
Примеры распределений отобранных событий по параметру аппроксимации x1.
Слева с ρ-отбором, справа без него.
Проблема ρ
Влияние отбора по ρ на распределения по параметру аппроксимации x1.
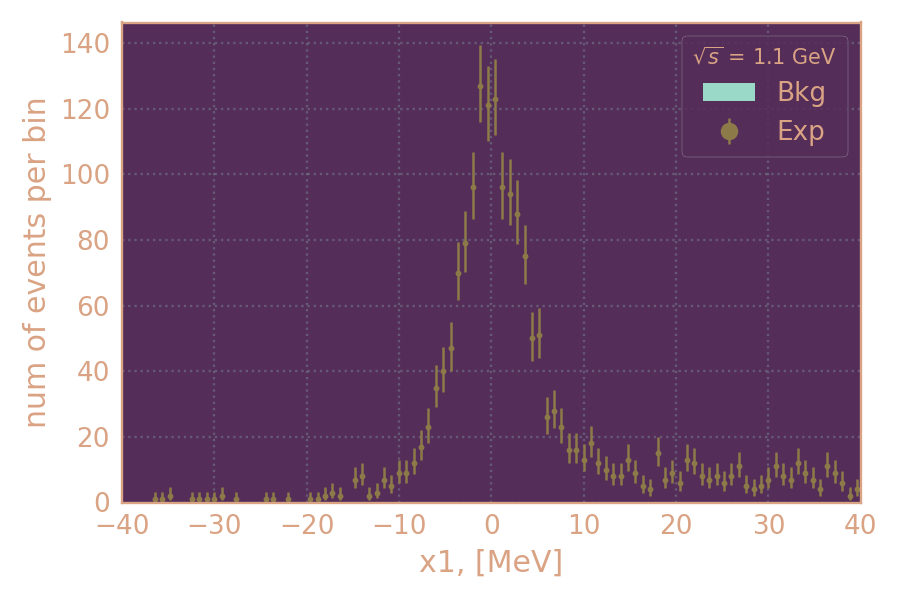
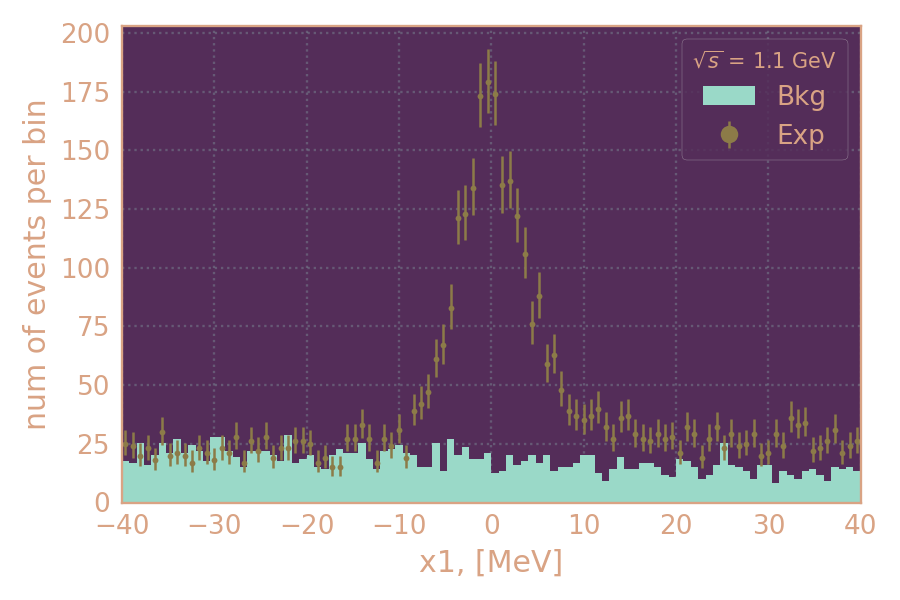
Примеры распределений отобранных событий по параметру аппроксимации x1.
Слева с ρ-отбором, справа без него.
Проблема ρ



(Ре) - Анализ процесса e+e– ➝ KSKL
В работе использовались данные 2011, 2012, 2017, 2019 и 2020 гг. с интегралом светимости 193 пб-1.
Критерии отбора событий
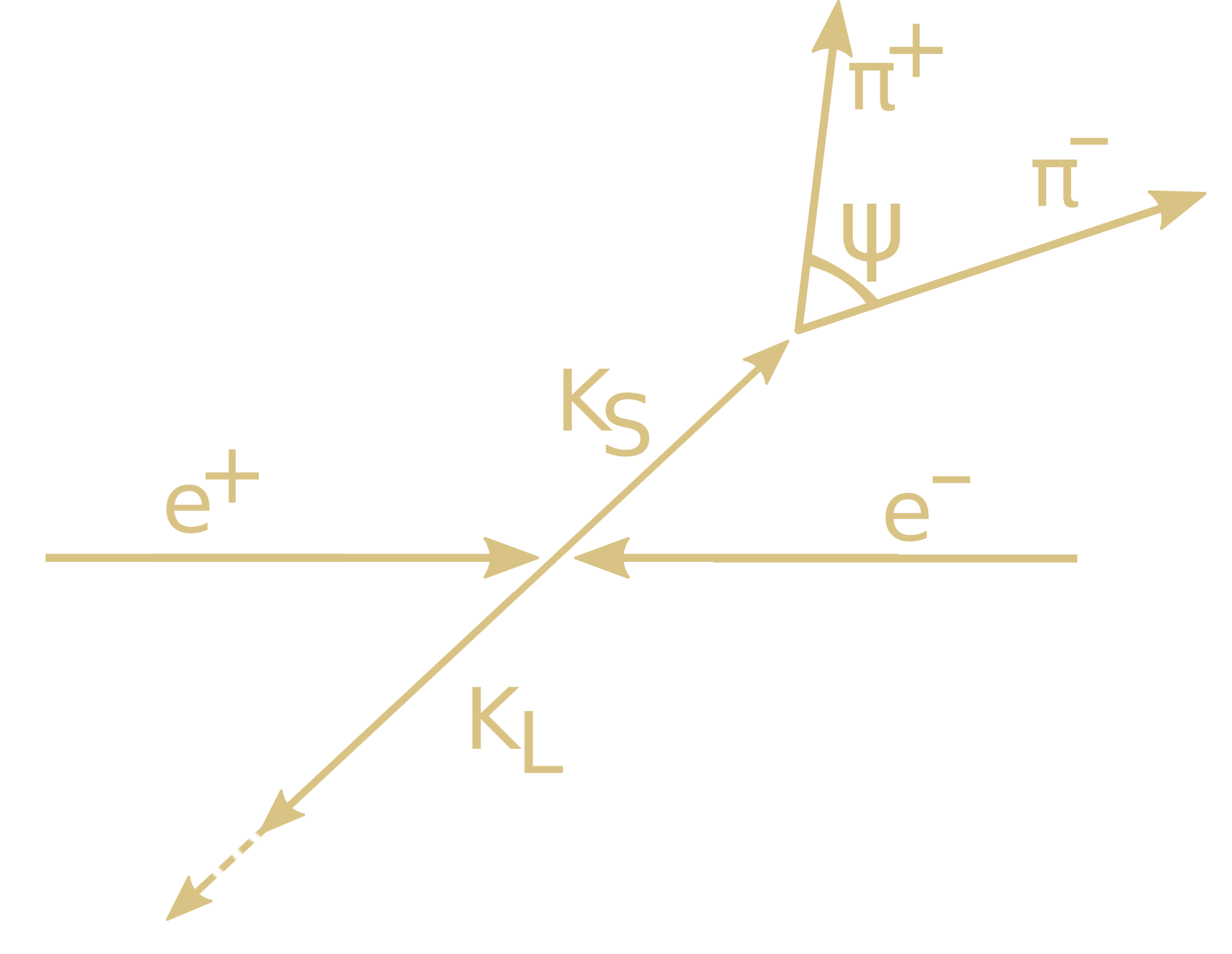
Схема изучаемого процесса
KS отбираются по распаду KS ➝ π+π− среди двухтрековых событий.
Каждый из треков соответствует условиям:
- |z| < 12 см
|ρ| > 0,1 см- |p| > 40 МэВ
- Число сработавших
проволочек > 6 - χr2 < 15; χz2 < 10
- dE/dX этих треков соответствует
ионизационным потерям пионов
Критерии отбора событий
KS отбираются по распаду KS ➝ π+π− среди двухтрековых событий.
Каждый из треков соответствует условиям:
- |z| < 12 см
|ρ| > 0,1 см- |p| > 40 МэВ
- Число сработавших
проволочек > 6 - χr2 < 15; χz2 < 10
- dE/dX этих треков соответствует
ионизационным потерям пионов
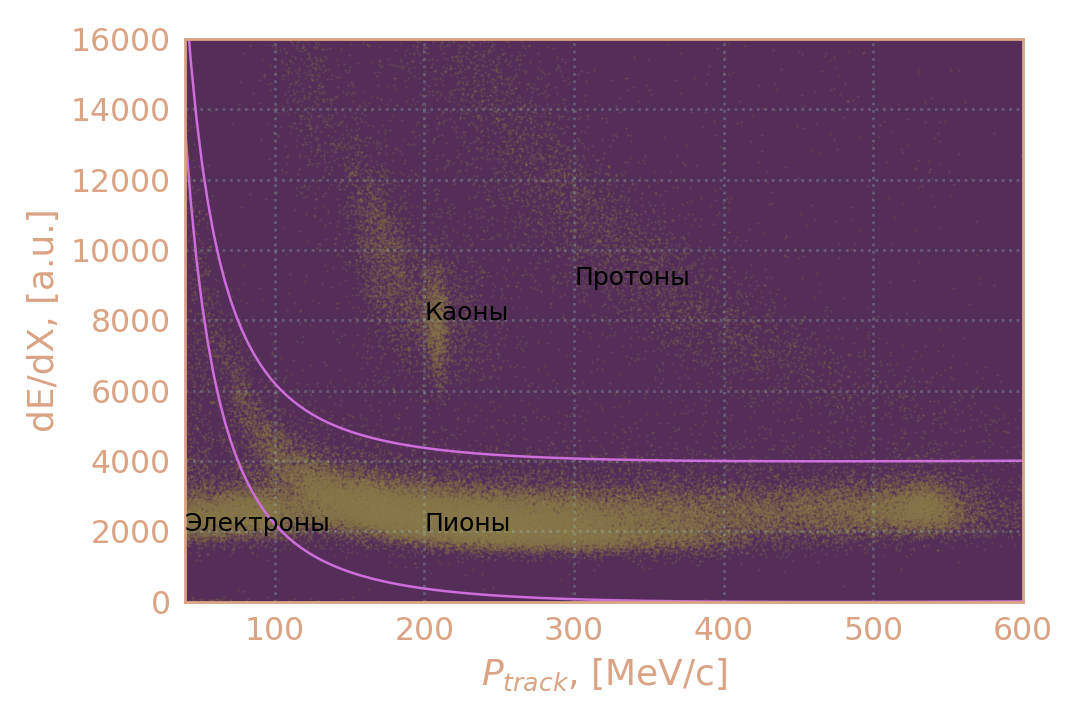
Распределение событий по ионизационным потерям в зависимости от импульса трека (выбираются события внутри линий)
Критерии отбора событий
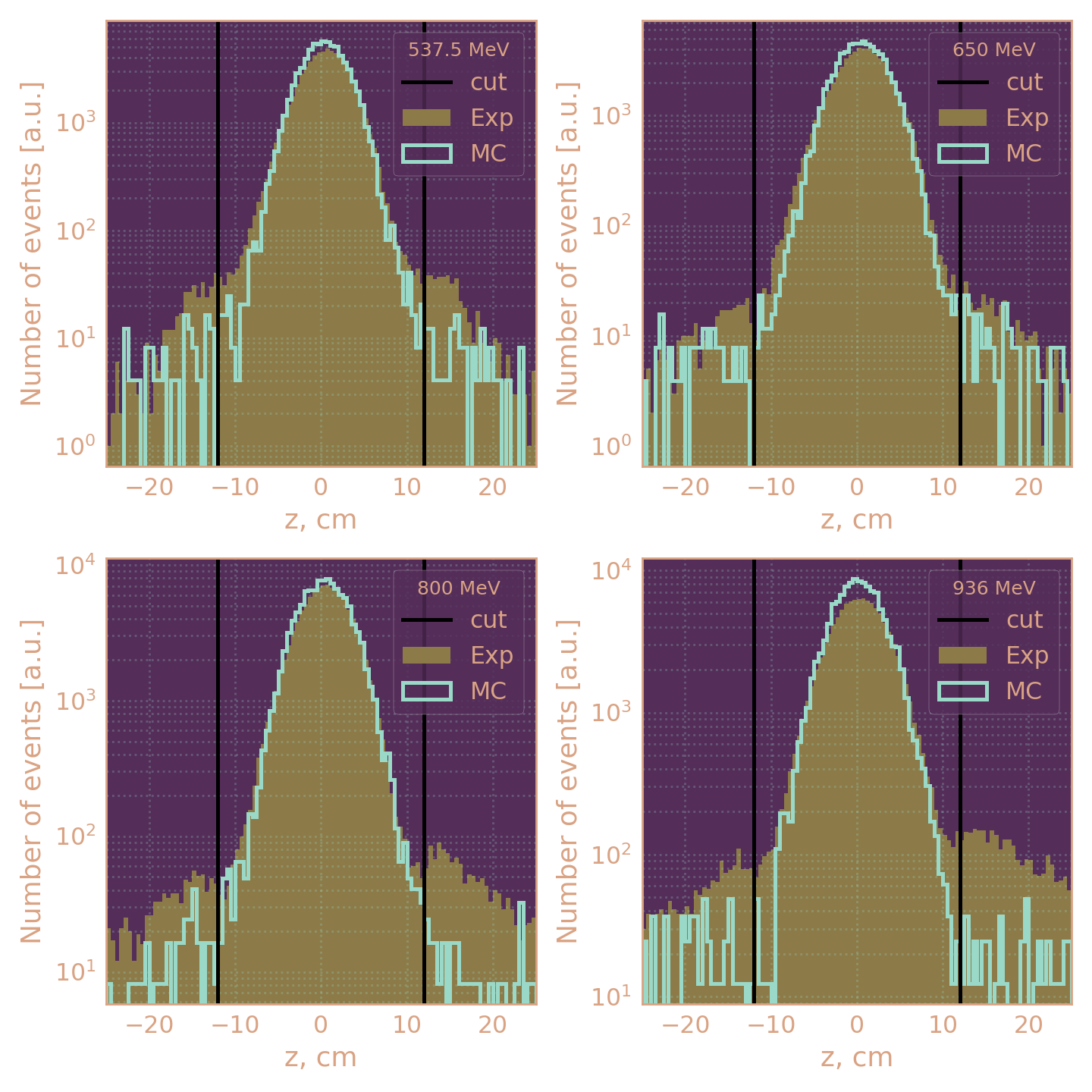
|z| < 12 см
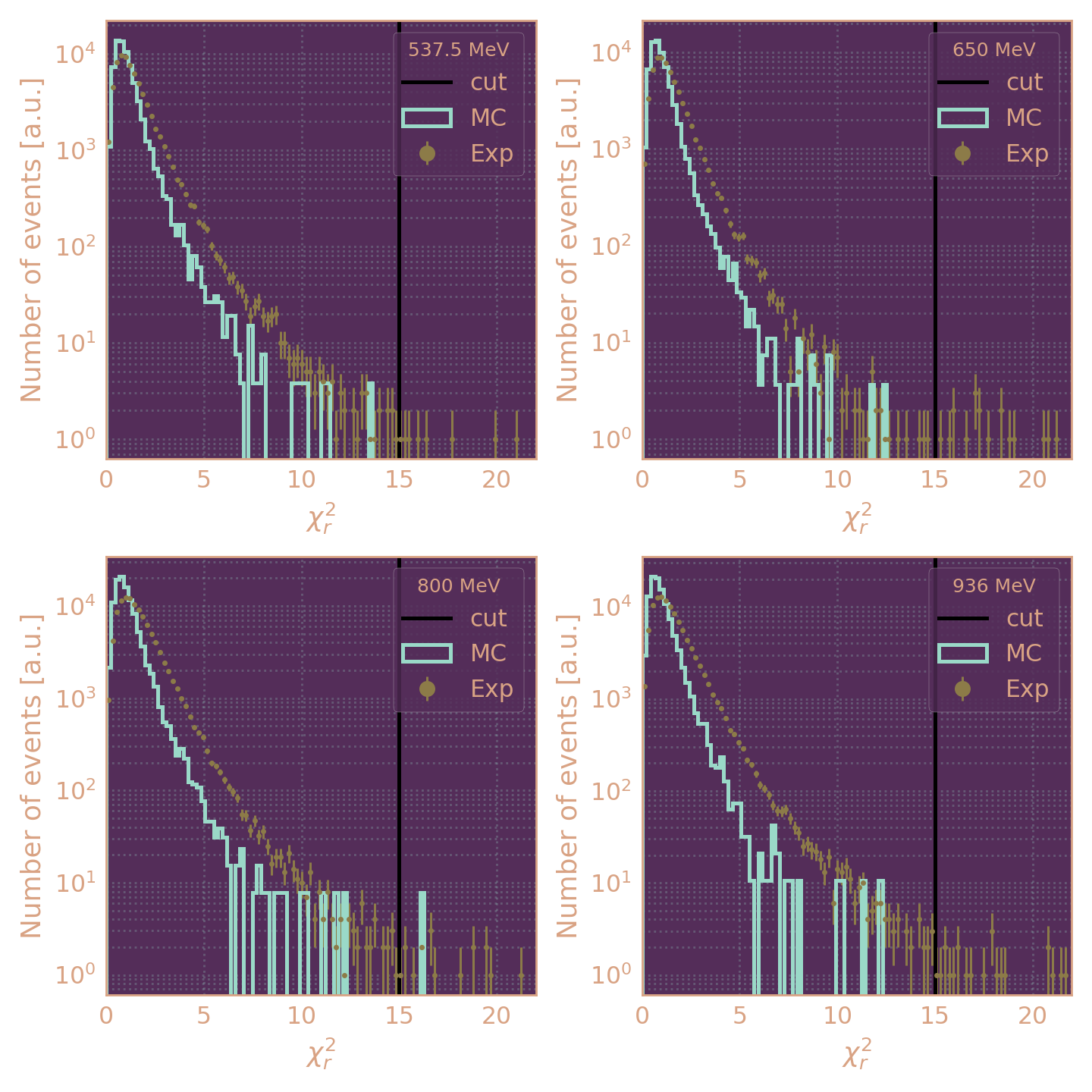
χr2 < 15
Критерии отбора событий

χr2 < 15
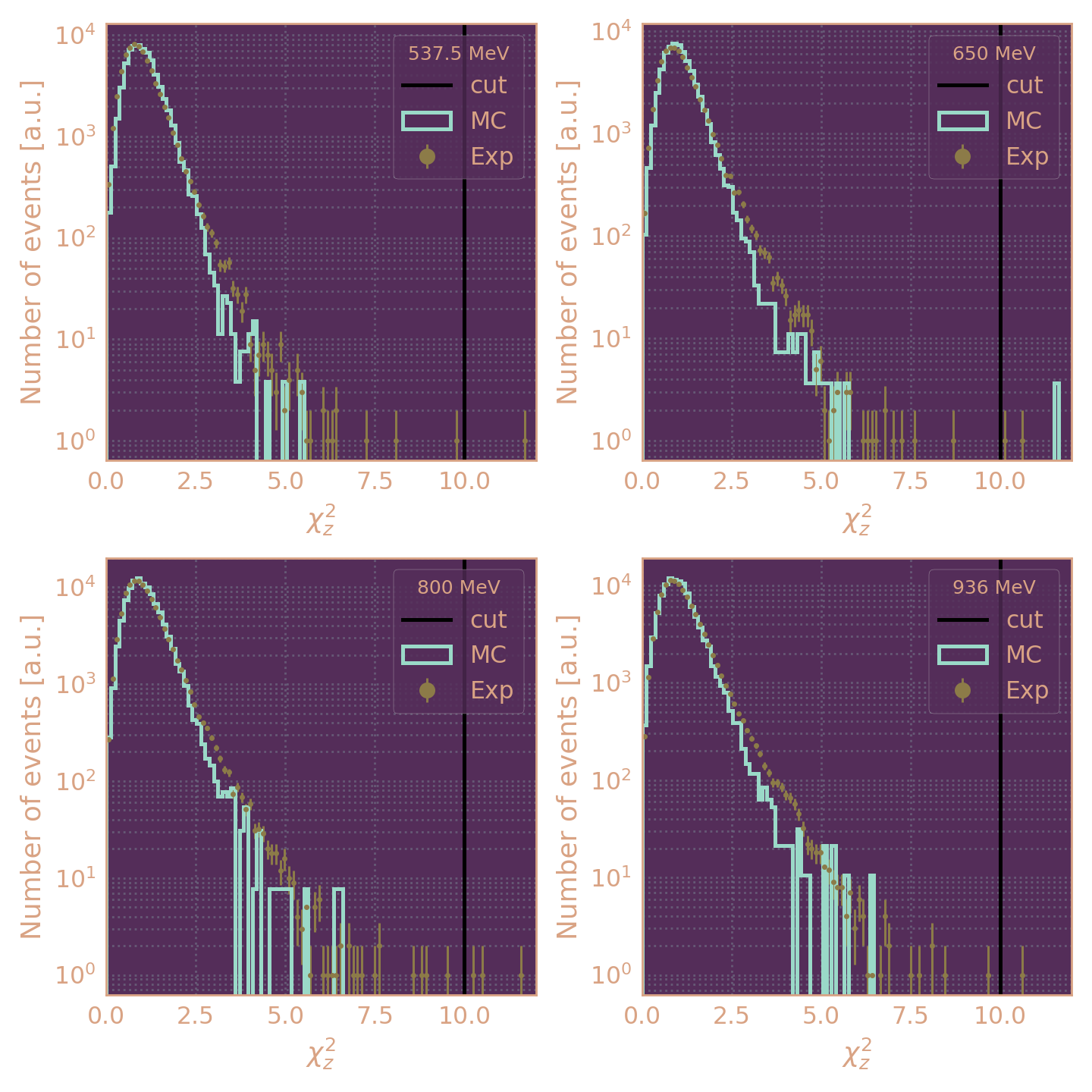
χz2 < 10
Критерии отбора событий
$$ dE/dx (\pi^{\pm}) = (161/\beta^2) \cdot \big( \ln(19275 \cdot \gamma^2 \beta^2) - \beta^2 \big) $$
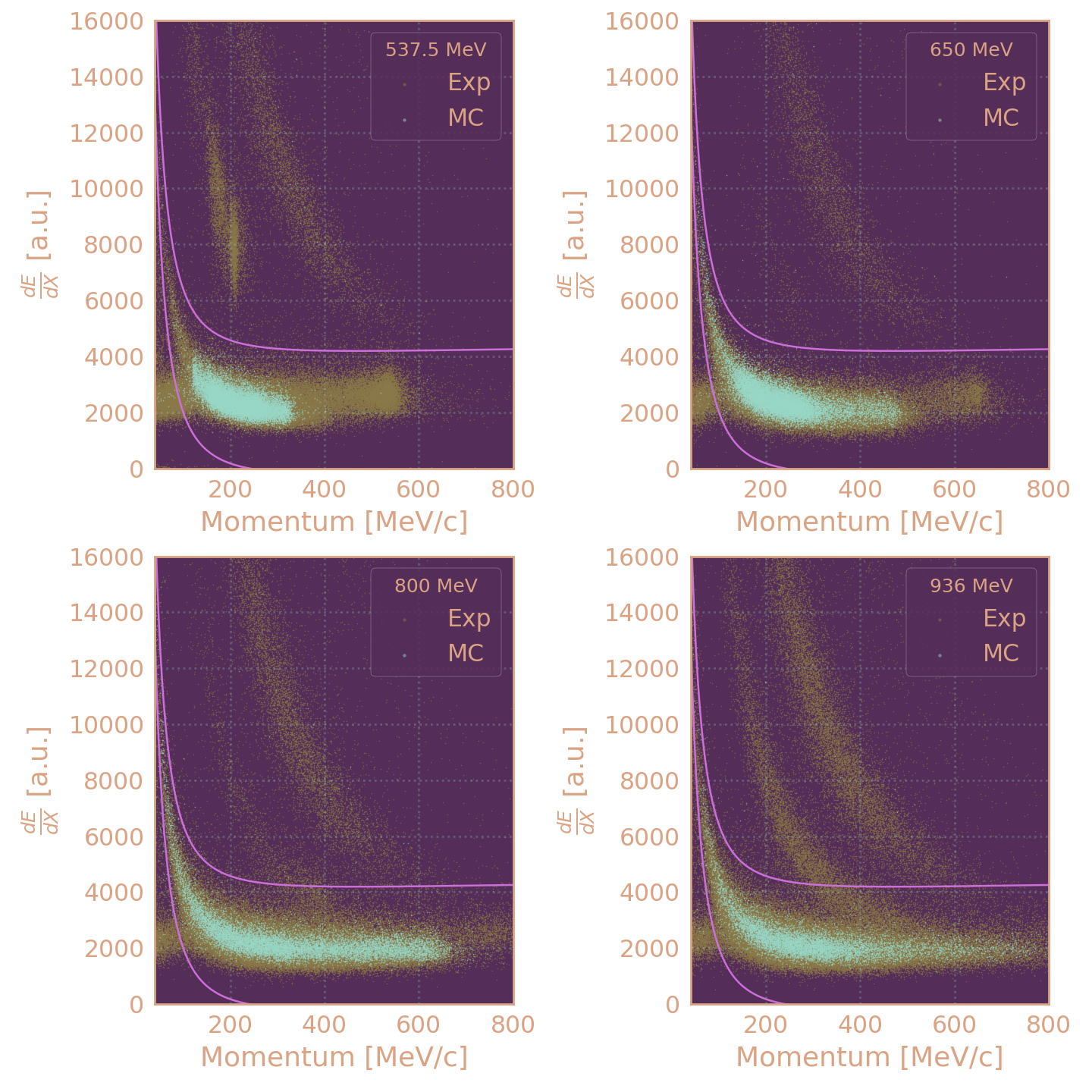
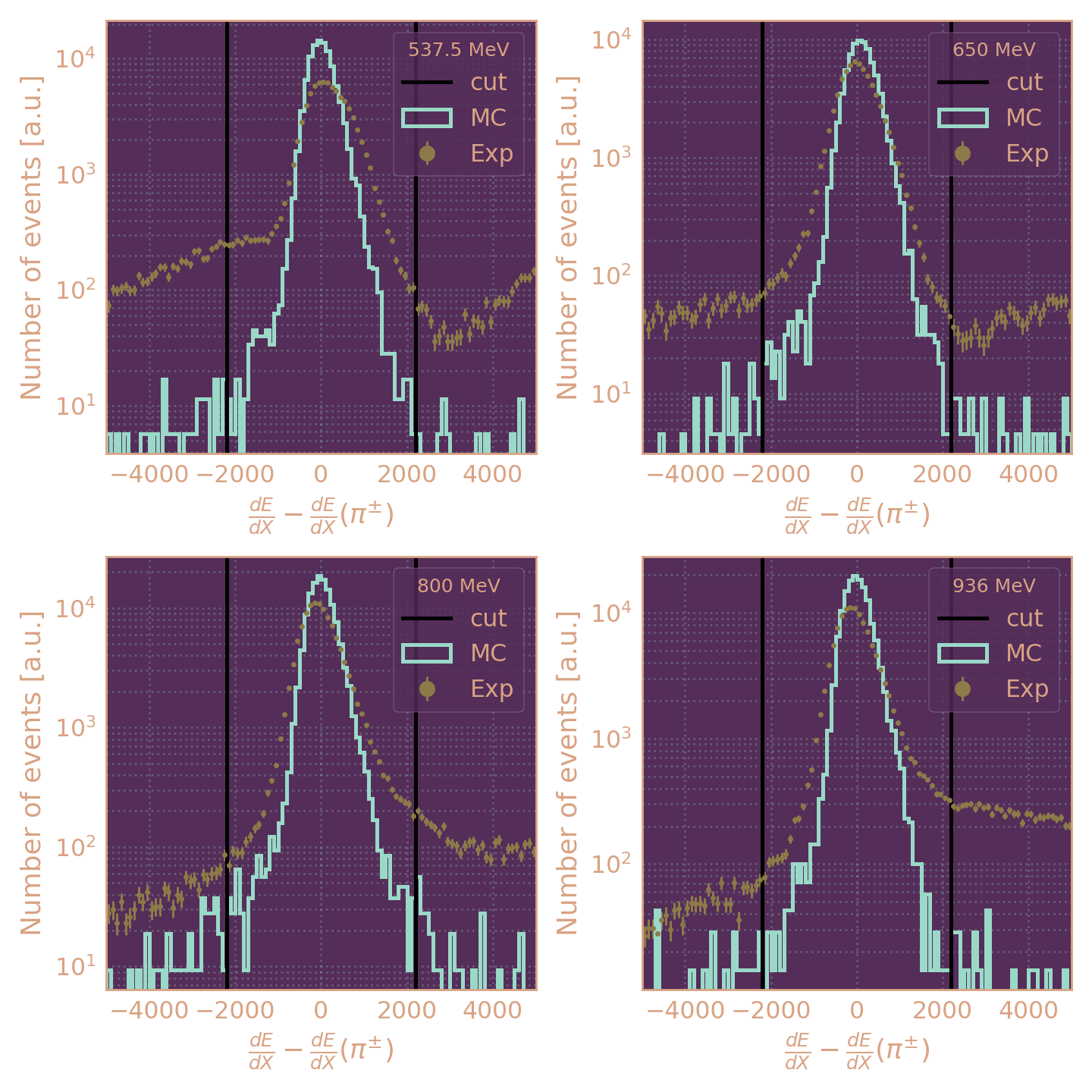
Критерии отбора событий

Схема изучаемого процесса
Критерий отбора по импульсу π± — углу разлёта распадных пионов (ψ)
Критерии отбора событий
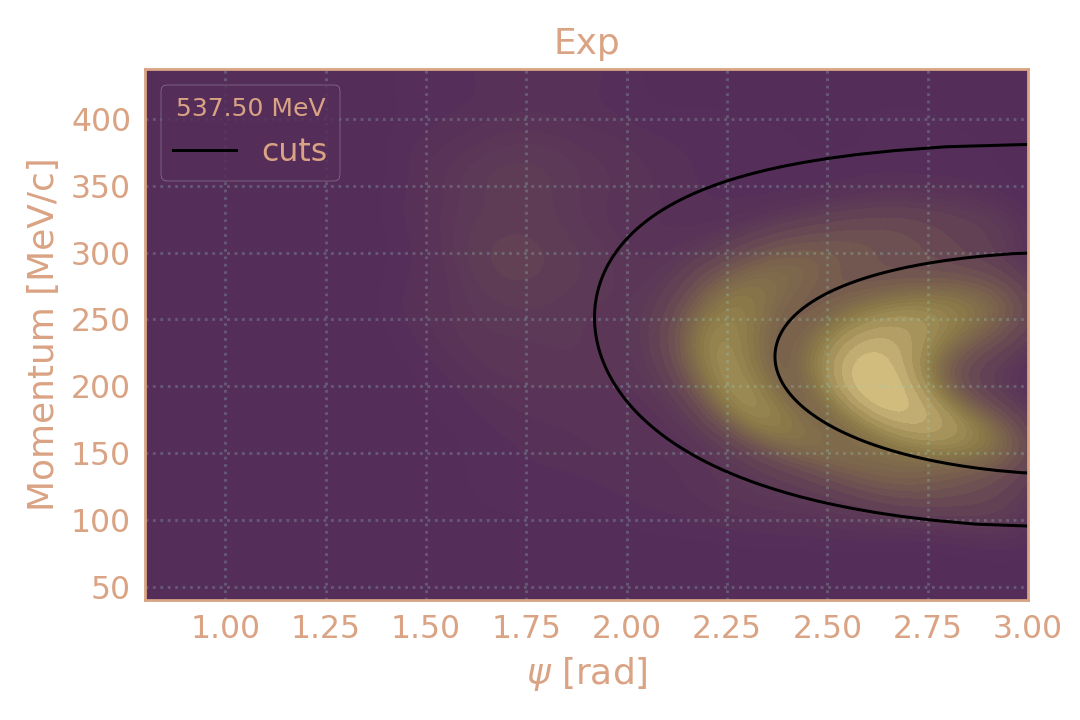
Распределение событий в эксп. (2019, 537.5 MeV) по импульсу π± в зависимости от угла разлёта (ψ). Чёрным обозначены критерии отбора.
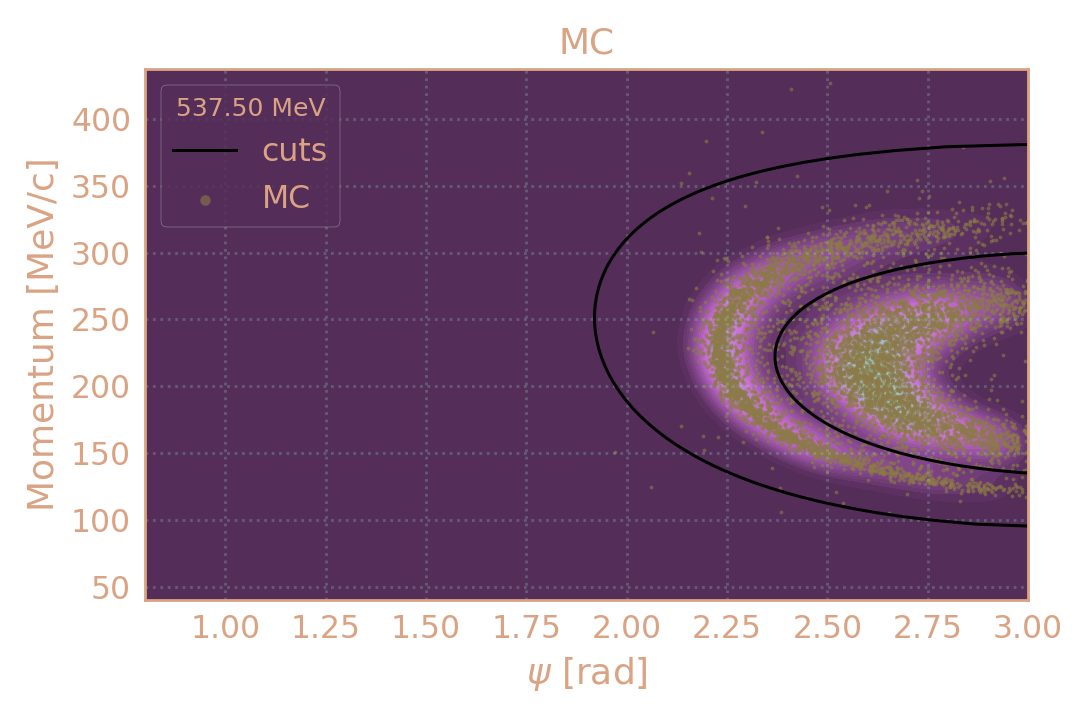
Распределение событий в MC (2019, 537.5 MeV) по импульсу π± в зависимости от угла разлёта (ψ). Чёрным обозначены критерии отбора.
Критерии отбора событий
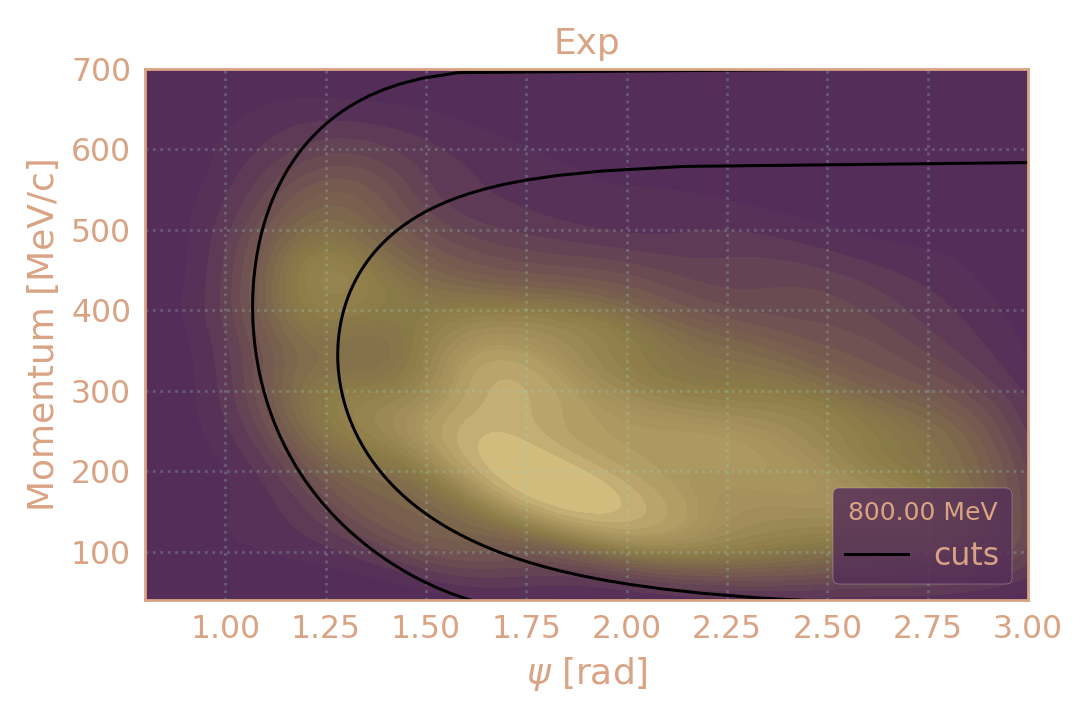
Распределение событий в эксп. (HIGH19, 800 MeV) по импульсу π± в зависимости от угла разлёта (ψ). Чёрным обозначены критерии отбора.
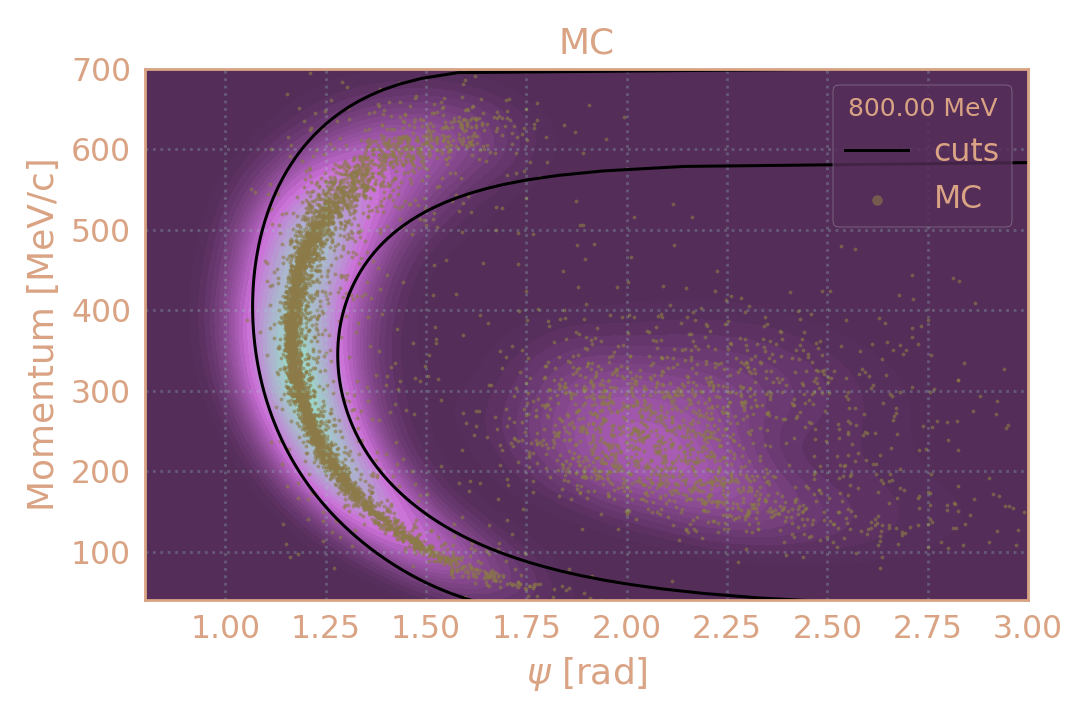
Распределение событий в MC (HIGH19, 800 MeV) по импульсу π± в зависимости от угла разлёта (ψ). Чёрным обозначены критерии отбора.
Критерии отбора событий
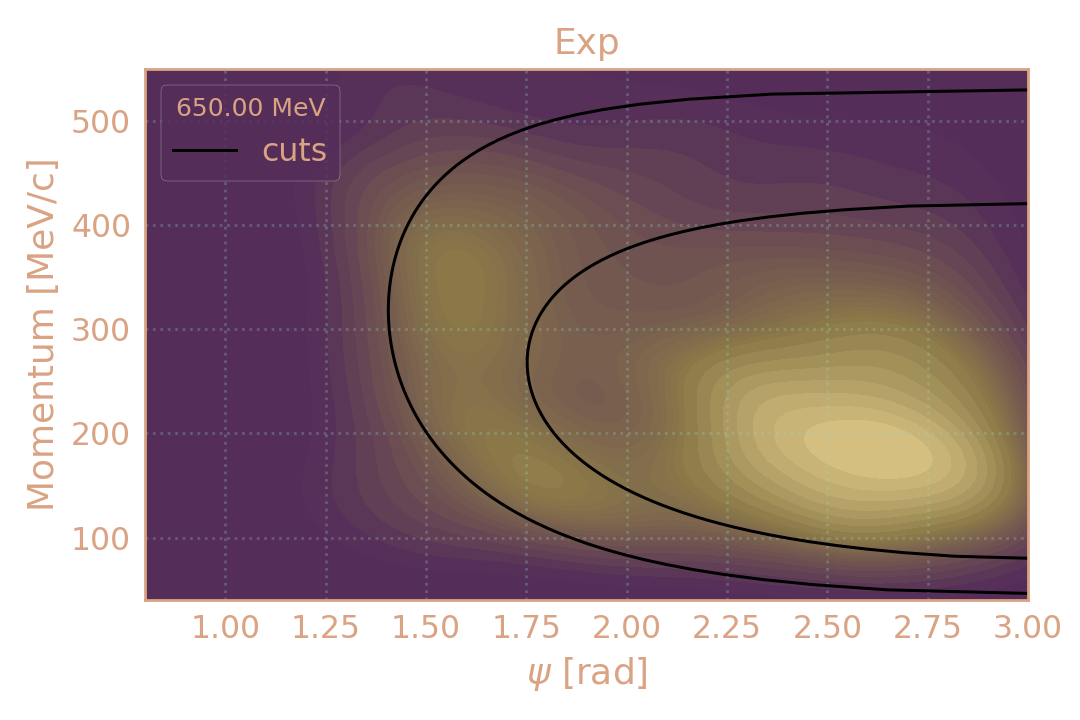
Распределение событий в эксп. (HIGH19, 650 MeV) по импульсу π± в зависимости от угла разлёта (ψ). Чёрным обозначены критерии отбора.
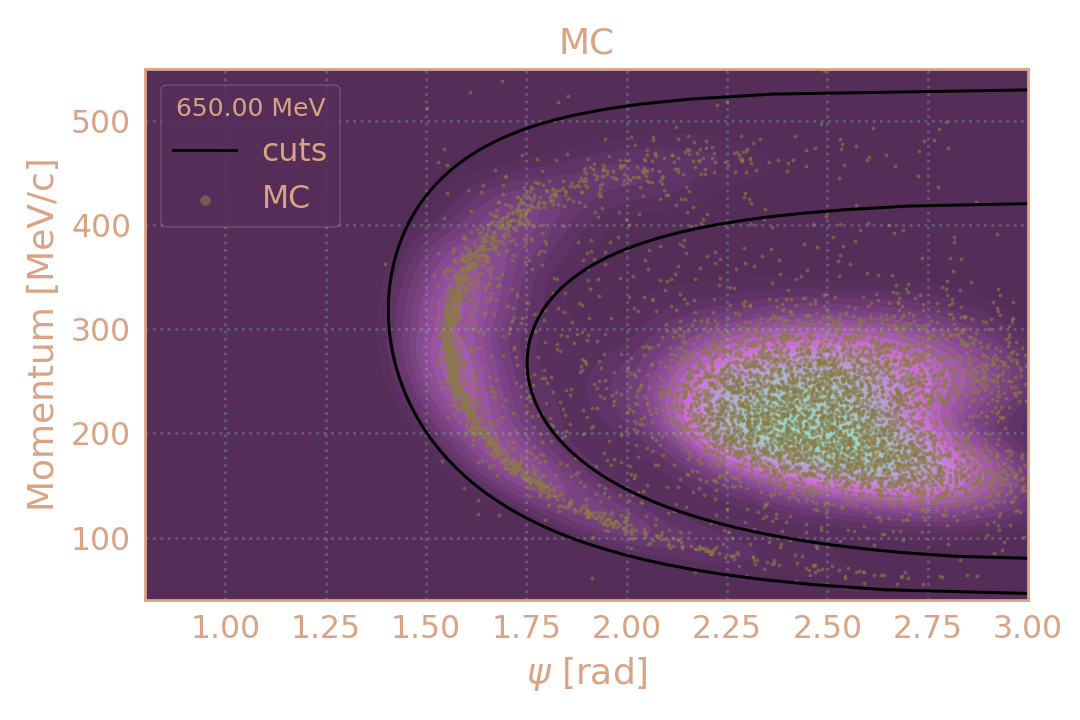
Распределение событий в MC (HIGH19, 650 MeV) по импульсу π± в зависимости от угла разлёта (ψ). Чёрным обозначены критерии отбора.
Критерии отбора событий
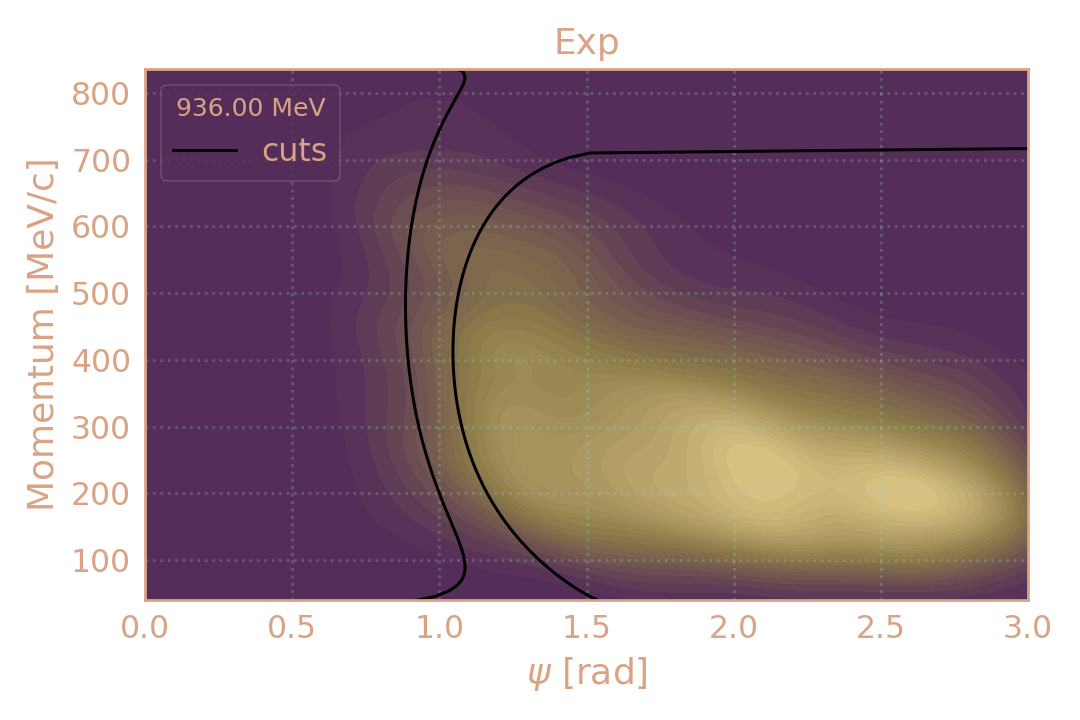
Распределение событий в эксп. (HIGH19, 936 MeV) по импульсу π± в зависимости от угла разлёта (ψ). Чёрным обозначены критерии отбора.
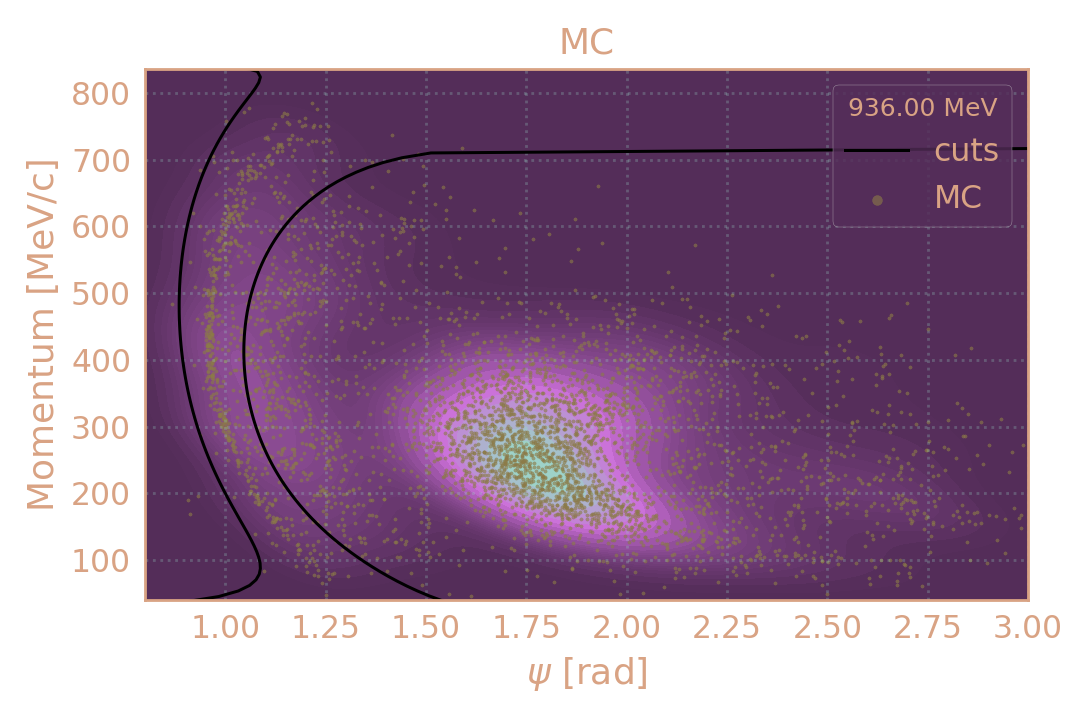
Распределение событий в MC (HIGH19, 936 MeV) по импульсу π± в зависимости от угла разлёта (ψ). Чёрным обозначены критерии отбора.
Критерии отбора событий
Отбор по углу (
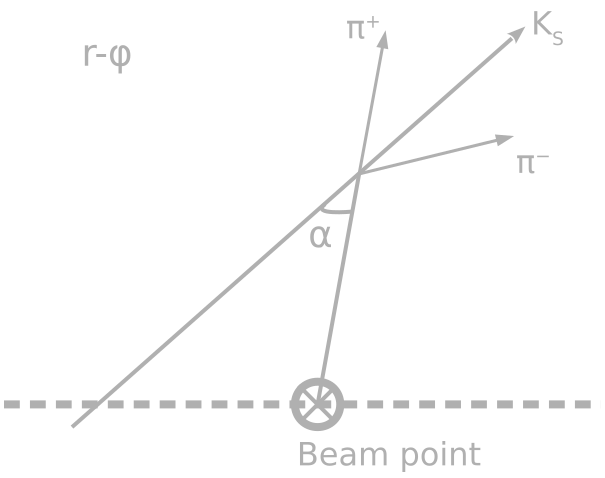
Схема с определением угла α
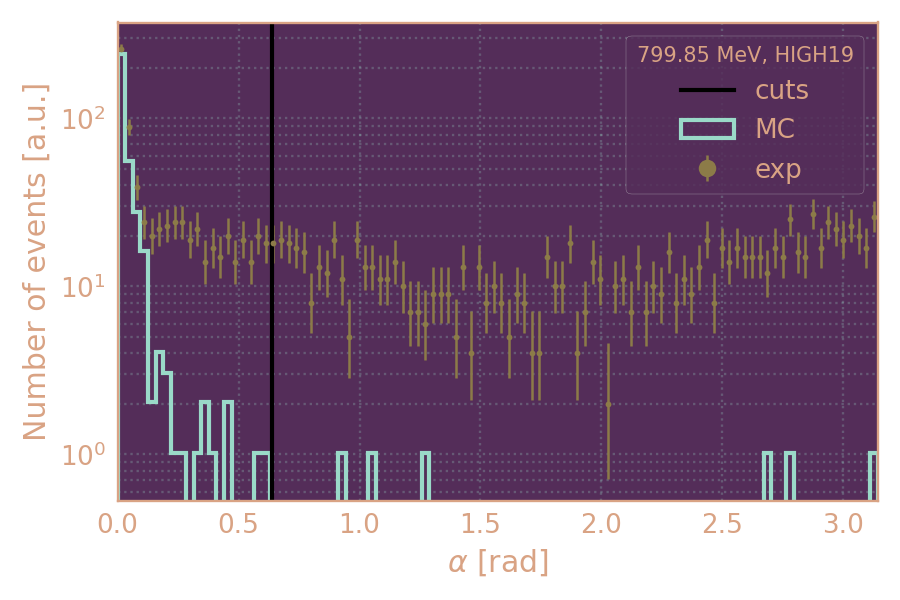
Распределение событий в эксп. и MC по углу α (2019, 800 MeV)
Критерии отбора событий
α < 0.64
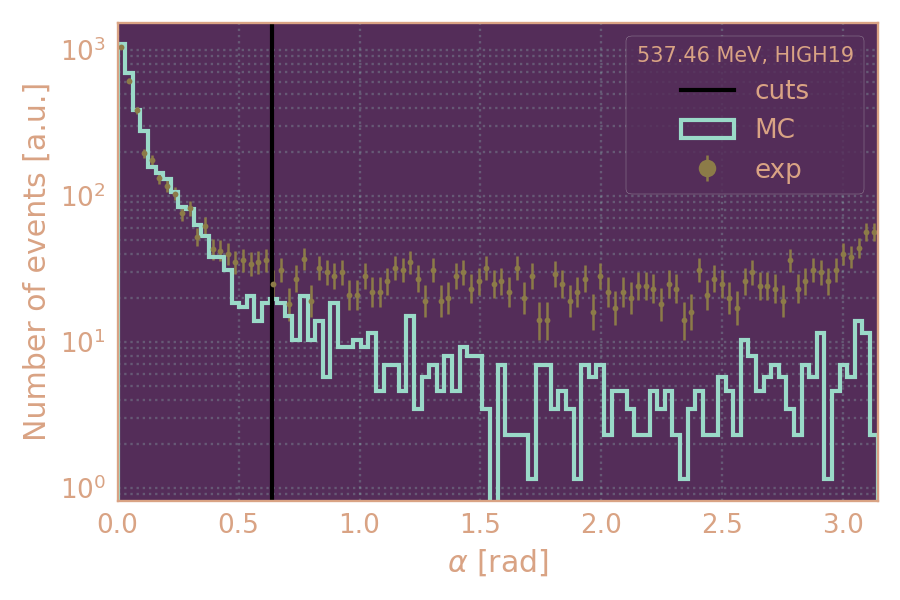
Распределение событий в эксп. и MC по углу α (HIGH19, 537.5 MeV)
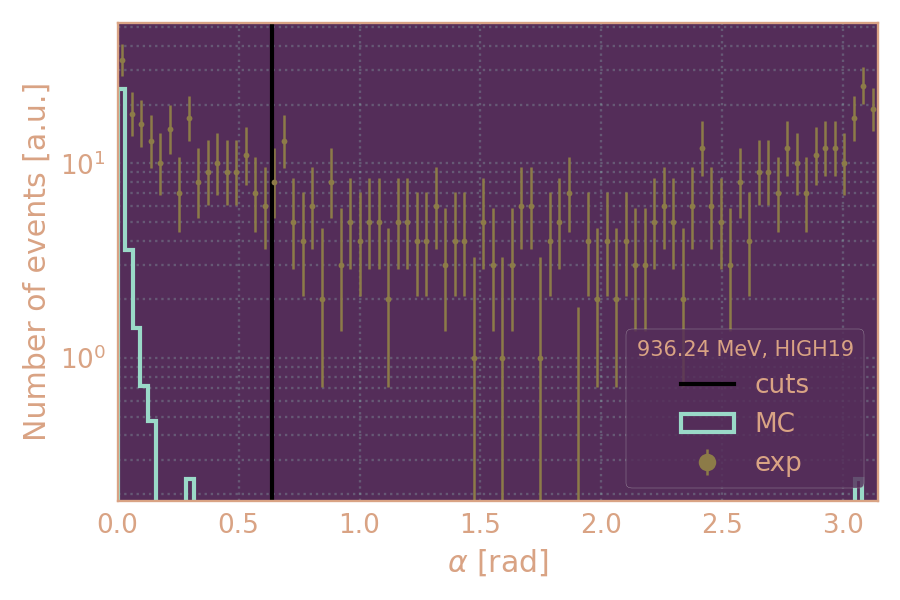
Распределение событий в эксп. и MC по углу α (HIGH19, 936 MeV)
Критерии отбора событий
Избавляюсь от фона
с помощью отбора на инвариантную массу пары фотонов.
Удаляется область:
- |mγγ - mπ0| < 70 MeV/c2
- Отлёт KS < 0.4 cm
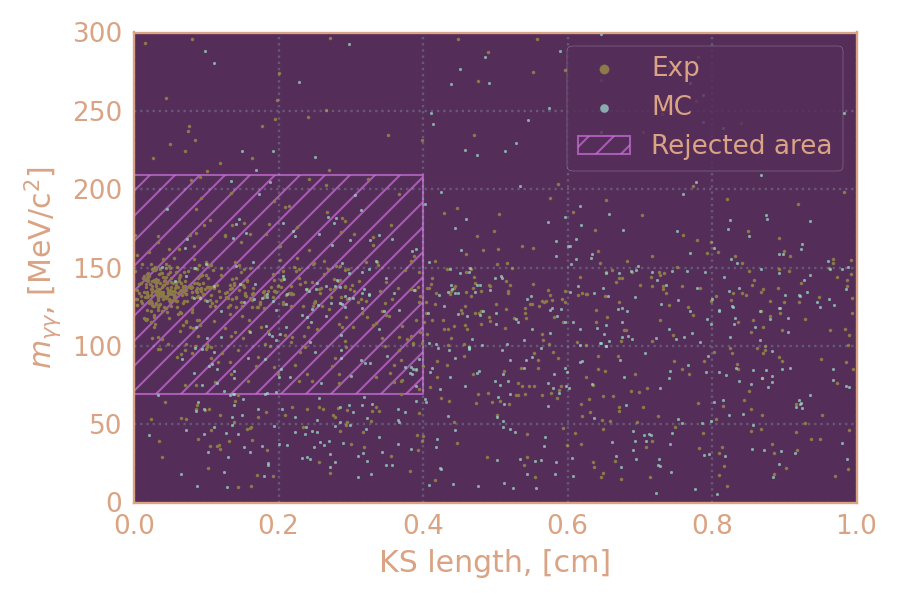
Распределение событий в эксп. и MC сигнального процесса (2019, 550 MeV) по инв. массе двух фотонов в зависимости от отлёта KS-кандидата. Чёрным выделена удалённая область.
Критерии отбора событий
Избавляюсь от фона
с помощью отбора на инвариантную массу пары фотонов.
Удаляется область:
- |mγγ - mπ0| < 70 MeV/c2
- Отлёт KS < 0.4 cm
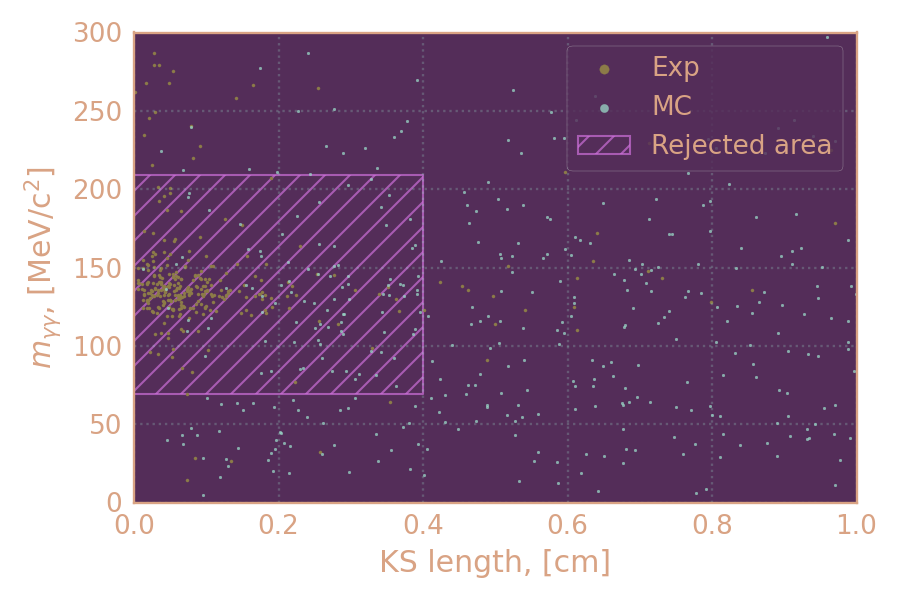
Распределение событий в эксп. и MC сигнального процесса (2019, 800 MeV) по инв. массе двух фотонов в зависимости от отлёта KS-кандидата. Чёрным выделена удалённая область.
Критерии отбора событий
Для отобранных событий строю распределение по инв. массе KS в зависимости от импульса KS, а затем поворачиваю на "угол корреляции".
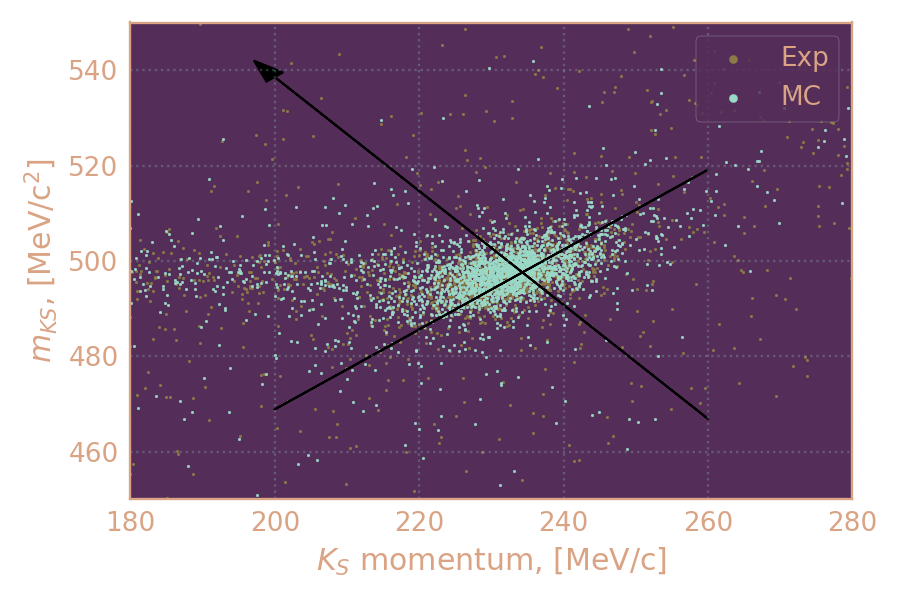
Распределение плотности событий в эксп. и MC (2019, 550 MeV) по инв. массе KS в зависимости от его импульса. Чёрным обозначены оси после поворота на "угол корреляции".
Критерии отбора событий
Для отобранных событий строю распределение по инв. массе KS в зависимости от импульса KS, а затем поворачиваю на "угол корреляции".
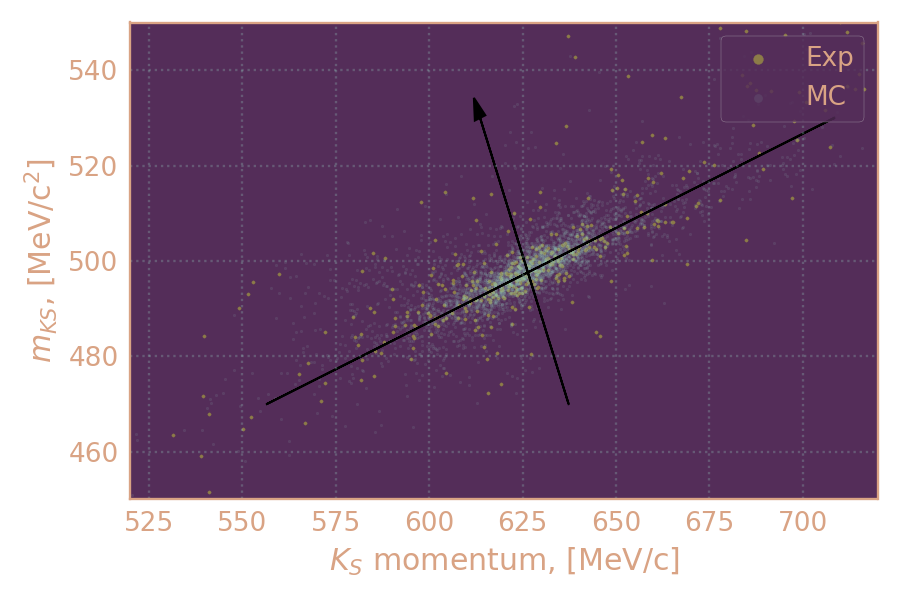
Распределение плотности событий в эксп. и MC (2019, 800 MeV) по инв. массе KS в зависимости от его импульса. Чёрным обозначены оси после поворота на "угол корреляции".
Критерии отбора событий
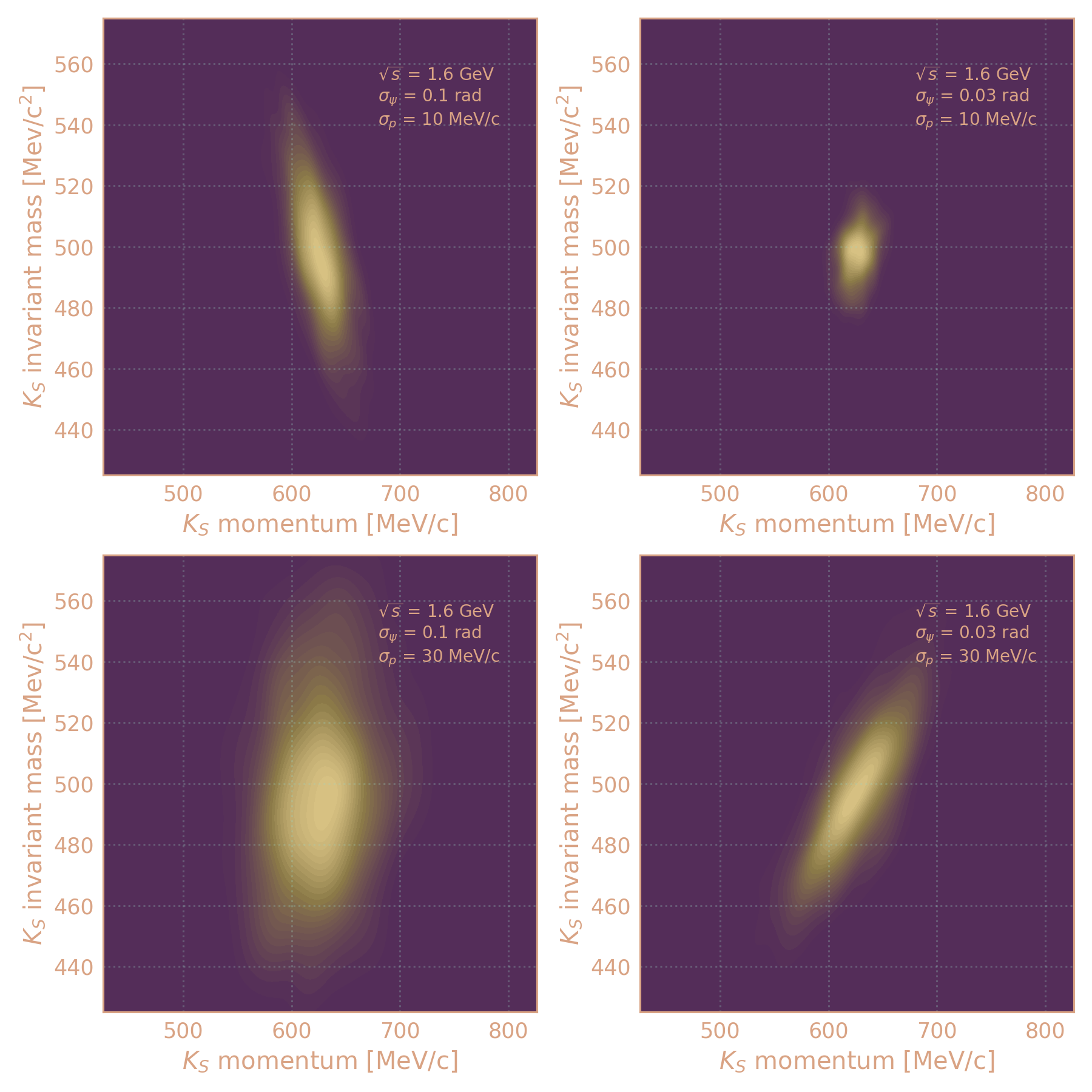
С помощью Toy MC показываю, что между вычисленной инв. массой и импульсом может быть корреляция:
$$M_K^2 = 2 M_{\pi}^2 + 2 ( \epsilon_+ \epsilon_- - p_+ p_- \cos\psi ) $$
$$p_K^2 = p_+^2 + p_-^2 + 2 p_+ p_- \cos\psi $$
В реальности $$\psi = \psi^0 + \delta\psi$$ $$p_\pm = p_\pm^0 + \delta p_\pm$$
Определение числа событий
Распределения событий по x1 аппроксимирую функцией: \[f \sim N_{sig} \cdot \text{g}(x, \mu, \sigma_L, \sigma_R, \alpha_L, \alpha_R) + N_{bkg} \]
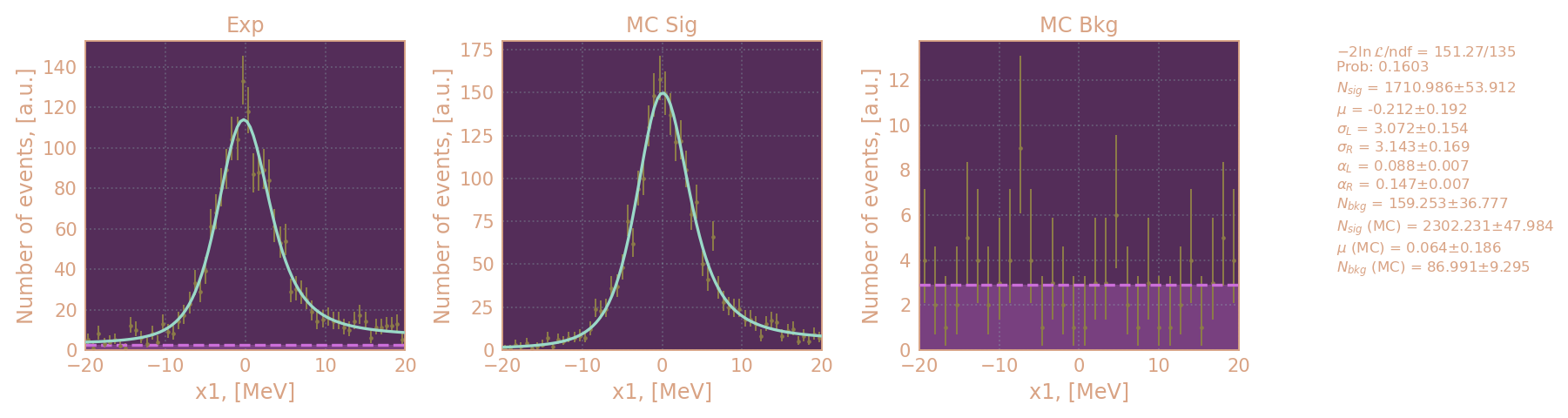
Распределение событий в по x1 в эксперименте, MC KSKL и MC фона (550 MeV) слева направо и аппроксимация.
Определение числа событий
Функция аппроксимации:
\[ \text{g}(x, \mu, \sigma_L, \sigma_R, \alpha_L, \alpha_R) \sim \begin{cases} \exp{\big(\frac{(x-\mu)^2}{2( \sigma_L^2 + \alpha_L (x-\mu)^2)}\big)}, x < \mu\\ \exp{\big(\frac{(x-\mu)^2}{2( \sigma_R^2 + \alpha_R (x-\mu)^2)}\big)}, x \geq \mu \end{cases} \]
Определение числа событий
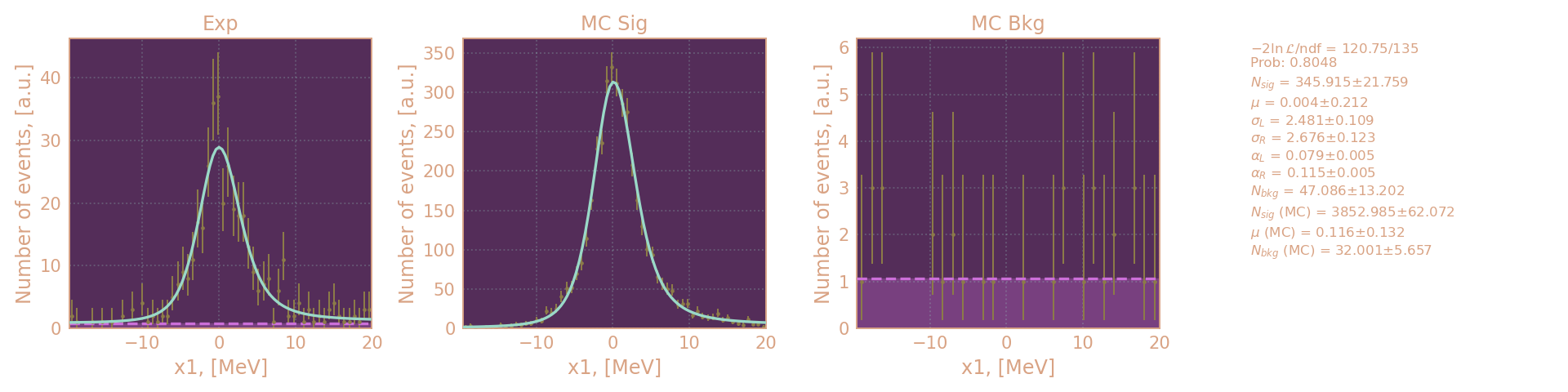
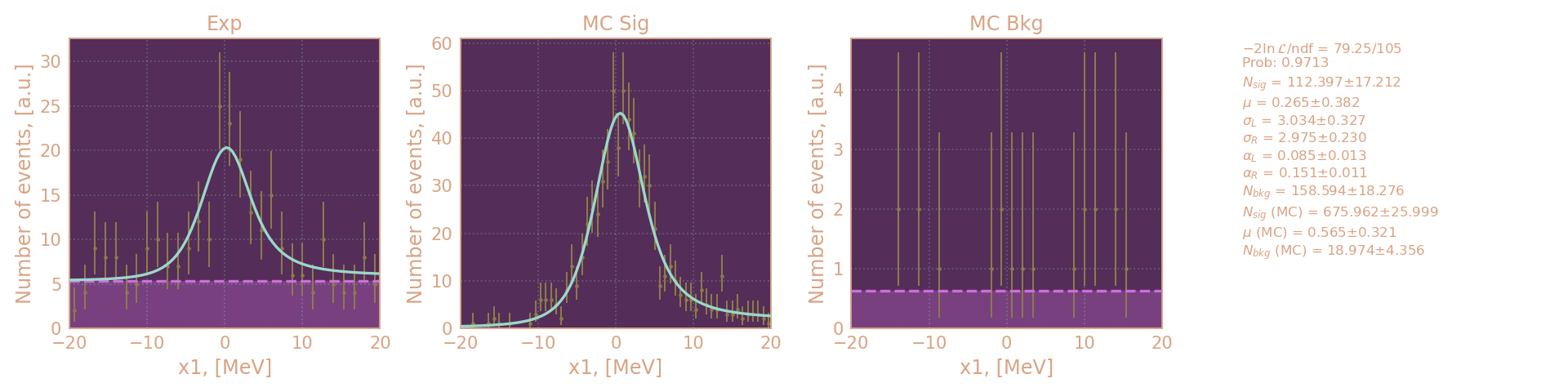
Распределение событий в по x1 в эксперименте, MC KSKL и MC фона (800 MeV сверху и 960 MeV снизу) слева направо и аппроксимация.
Эффективность реконструкции в ДК
Эффективность реконструкции треков, летящих в область ДК
Выбираю среди сигнальных событий те, где хотя бы у одного трека подходящий θ. Сравниваю распределения по θ для второго трека в эксперименте и МС.
Отношение распределения в эксперименте и МС определяет поправку в зависимости от θ. События из МС перевзвешиваются с учётом поправки.
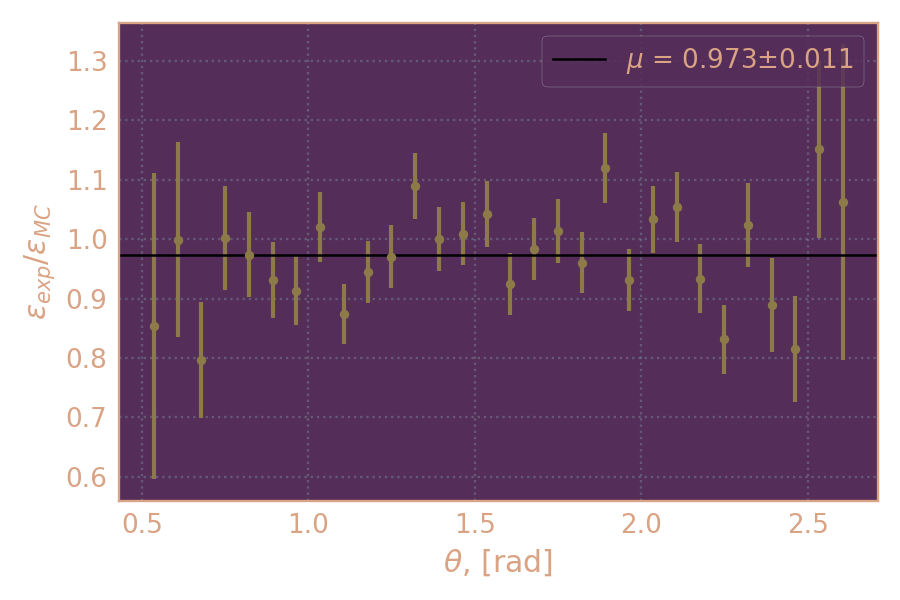
Поправка на эффективность реконструкции ДК в зависимости от θ (2019).
Поправка на эффективность ДК
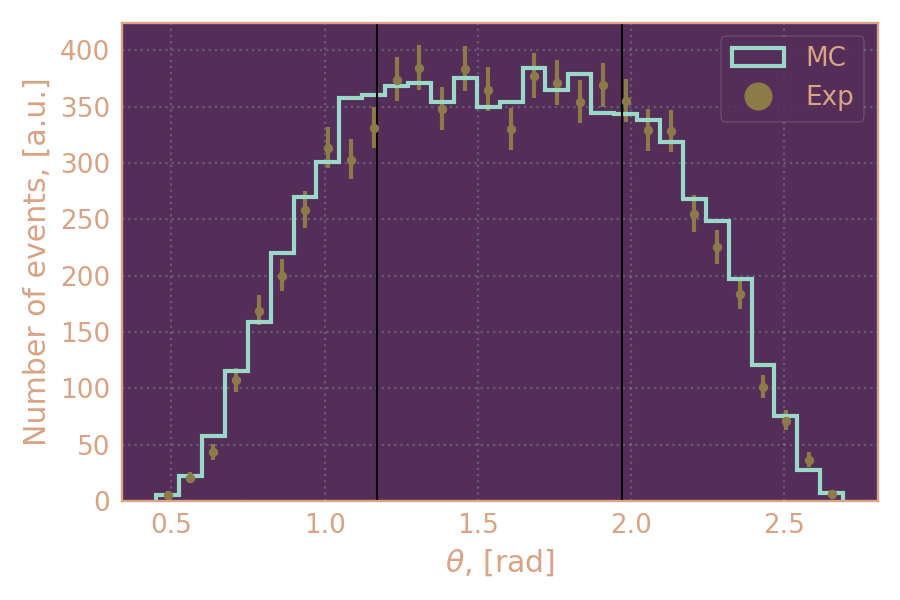
Сравнение распределений по полярному углу θ в эксперименте и МС. Чёрным обозначена область, где эффективность считалась одинаковой.

Поправка на эффективность реконструкции ДК в зависимости от θ.
Поправка на эффективность ДК
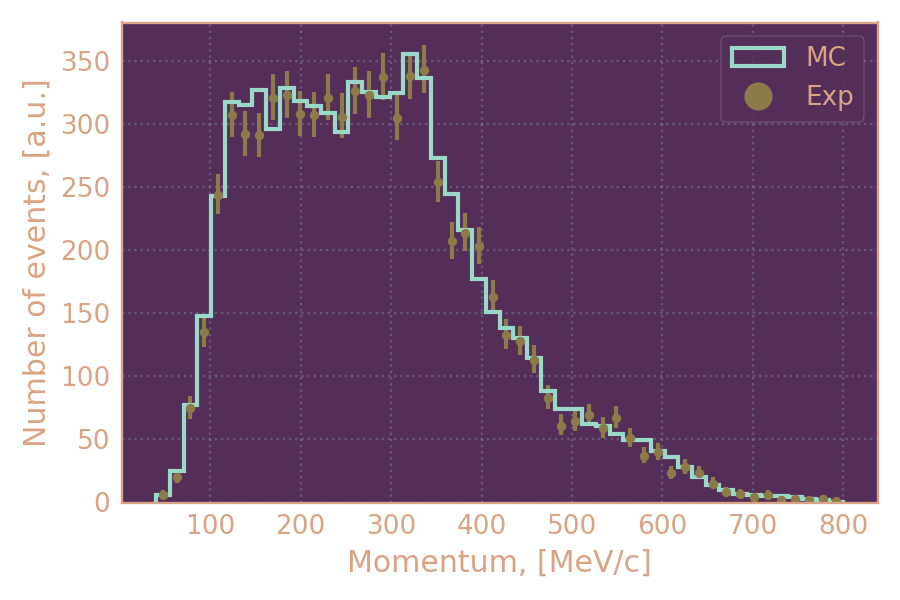
Распределение событий по импульсу второго трека в эксперименте и MC.
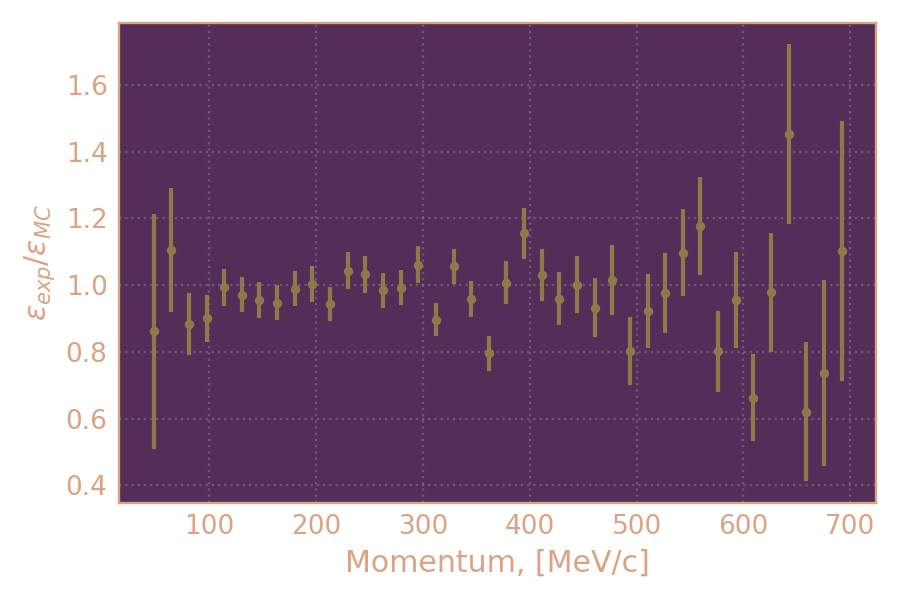
Поправка на эффективность ДК в зависимости от импульса. (Поправка считается независимой от импульса трека)
Эффективность реконструкции в ДК
проверка одинаковой эффективности для
Для этого выбираю события сигнального процесса по кластеру KL и треку-кандидату в заряженный π.
Эффективность реконструкции в эксперименте и МС определяется по формуле:
\[ \varepsilon_{rec} = \frac{1}{1 + N_1/N_2} \]
N1 - количество однотрековых событий
N2 - количество двухтрековых событий
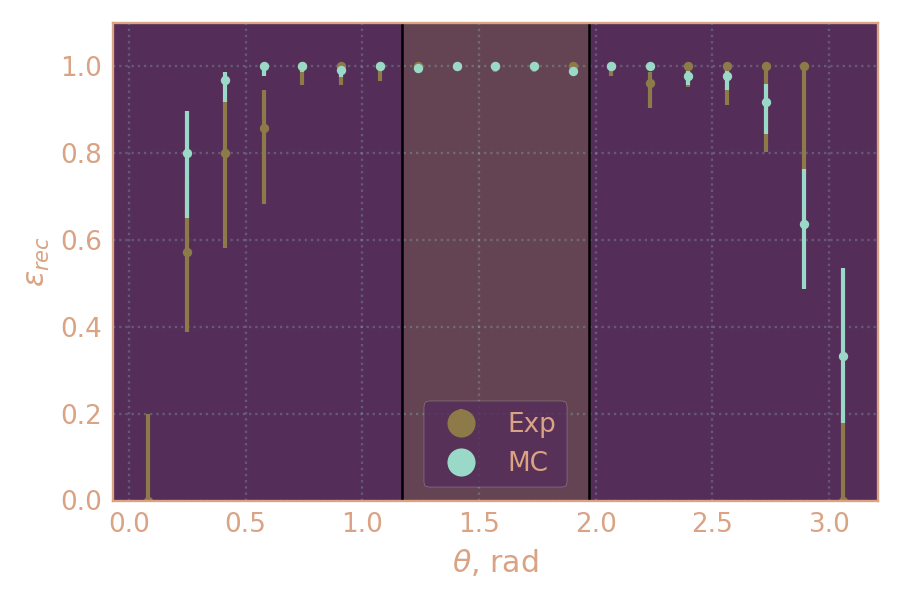
Поправка на эффективность реконструкции ДК в зависимости от θ.
В выделенной области
Эффективность триггеров
На КМД-3 работают два триггера: TF и CF.
В предположении их независимости эффективность вычисляется так:
\[ \varepsilon_{trig} = 1 - (1- \varepsilon_{TF}) (1 - \varepsilon_{CF}) \]
\[ \varepsilon_{TF} = \frac{N_{TF\&CF}}{N_{CF} + N_{TF\&CF}} \]
\[ \varepsilon_{CF} = \frac{N_{TF\&CF}}{N_{TF} + N_{TF\&CF}} \]
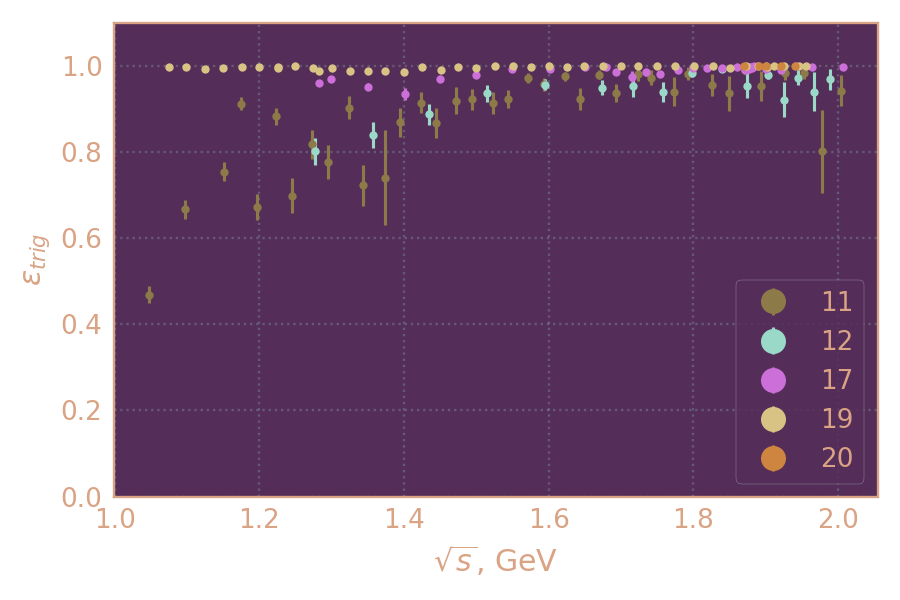
Эффективность триггеров в зависимости от энергии в с.ц.м.
Эффективность регистрации
в зависимости от энергии радиационного фотона
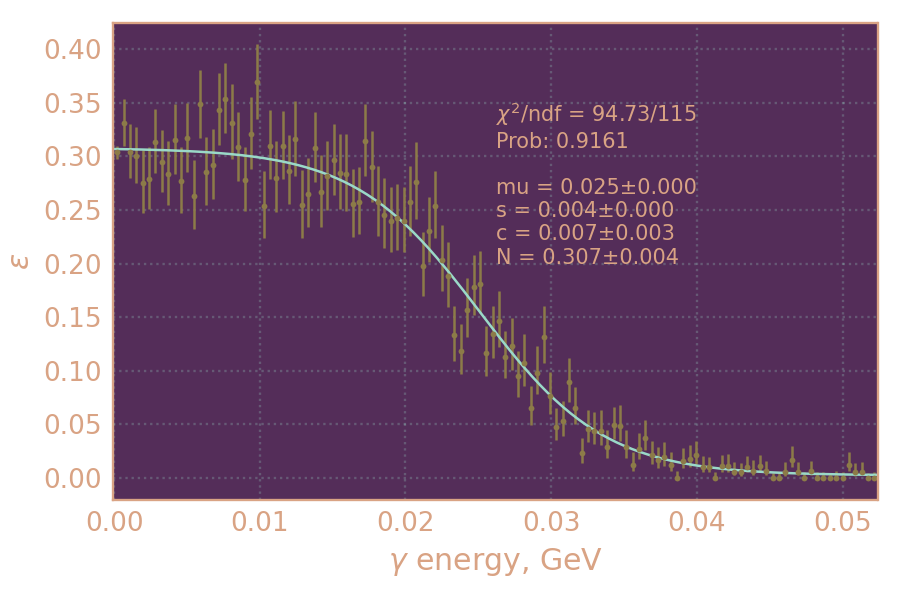
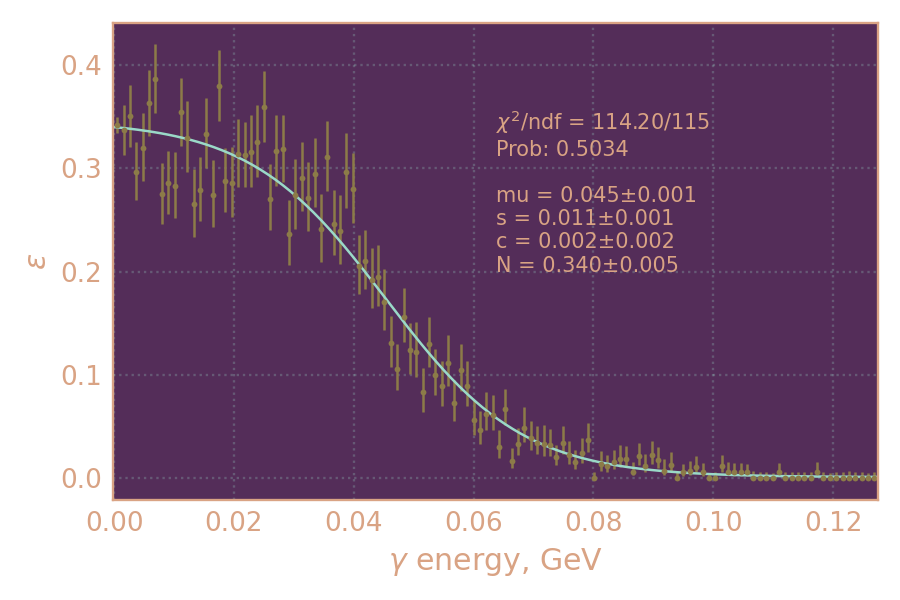
Определяю и аппроксимирую эффективность регистрации
в зависимости от энергии радиационного фотона для энергий 550 МэВ (слева) и 625 МэВ (справа)
(использую MC KSKL с равномерно распр. рад. фотоном)
Эффективность регистрации
в зависимости от энергии радиационного фотона
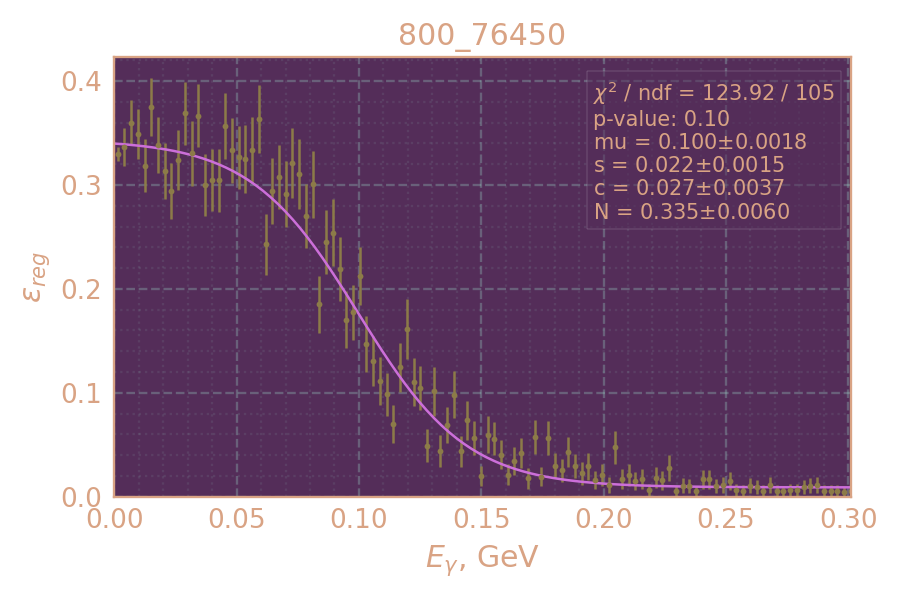
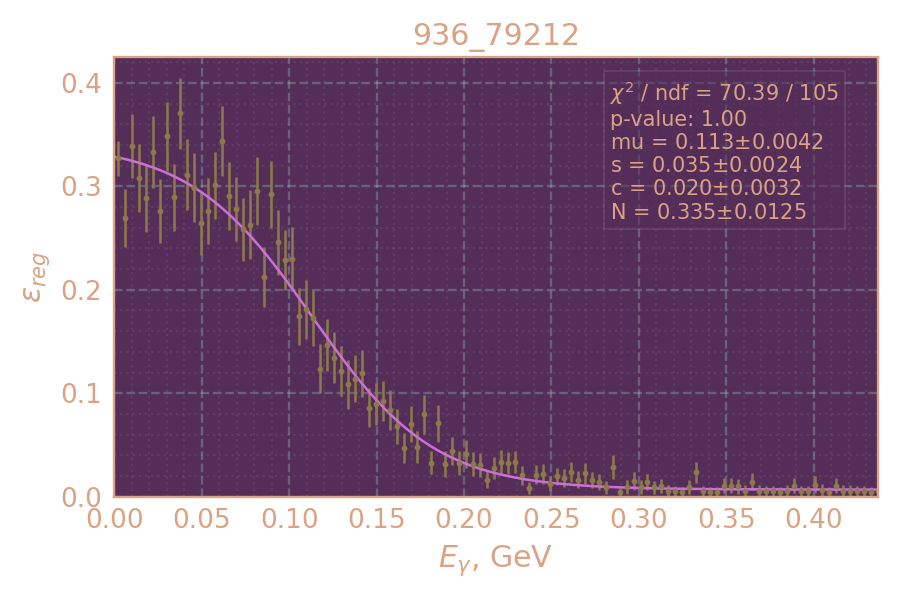
Определяю и аппроксимирую эффективность регистрации в зависимости от энергии радиационного фотона (использую MC KSKL с равномерно распр. рад. фотоном)
Эффективность регистрации и рад. поправки
Радиационная поправка определяется по формуле: \[ \sigma_{vis} = \int_0^1 F(x, s) \sigma_{born} (s [1-x]) \varepsilon_{reg}(x,s)dx = \sigma_{born} \varepsilon (1+\delta) \]
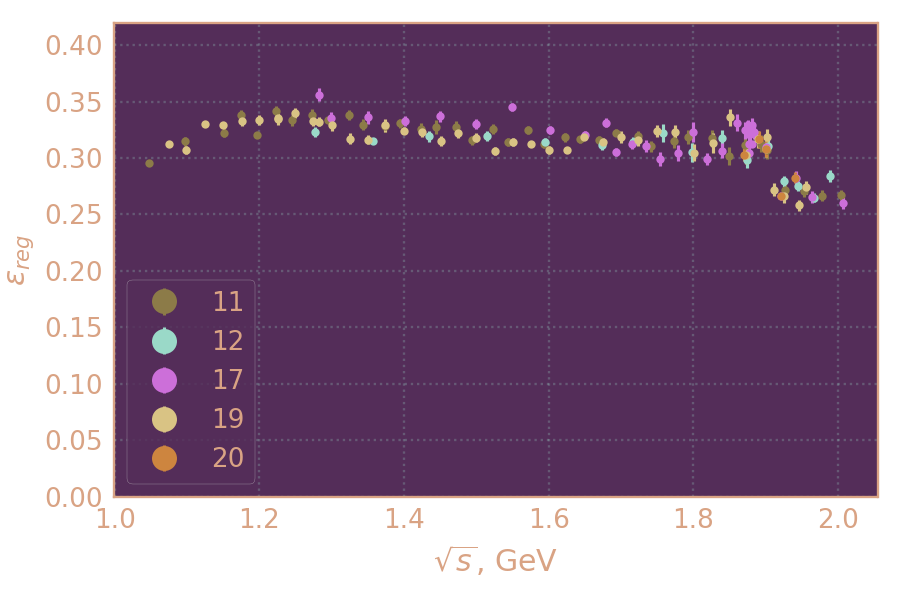
Эффективность регистрации для рад.фотона с нулевой энергией в зависимости от энергии в с.ц.м. по сезонам
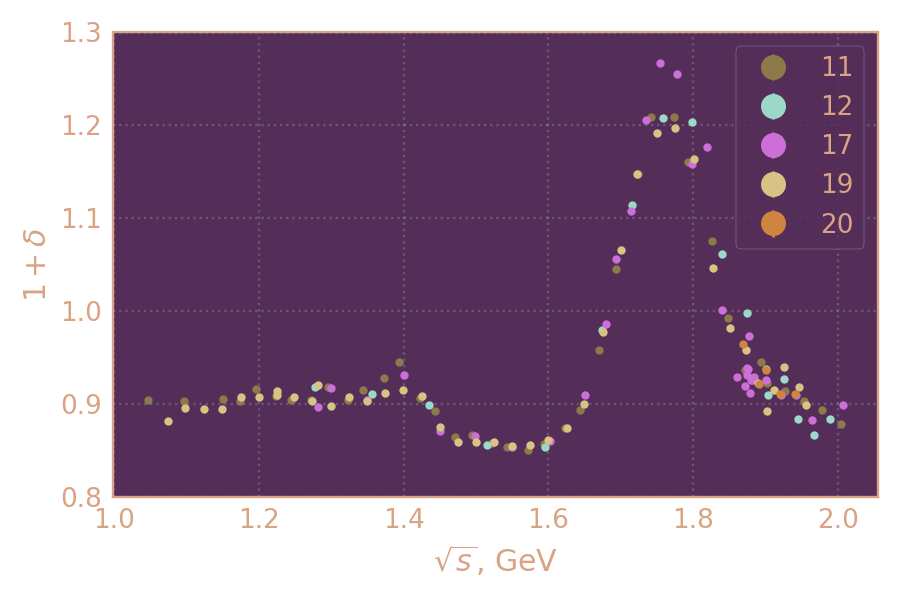
Рад.поправка в зависимости от энергии в с.ц.м. по сезонам
Сечение процесса
\[ \sigma_{born} = \frac{N_{sig}}{\varepsilon L (1 + \delta)} \]
Зависимость сечения процесса e+e– ➝ KSKL от энергии в с.ц.м. по сезонам в логарифмическом масштабе.
Систематические ошибки (статус)
| Отбор | Сист. погрешность (%) |
|---|---|
| по z | <0.1 |
| dE/dX | <0.2 |
| α | <0.5 |
| ψ-Pπ | 1 |
| π0 | 1 |
Заключение
Результаты
- Разработаны критерии отбора процесса e+e– ➝ KSKL
- Вычислены эффективности регистрации, реконструкции и рад.поправки
- Измерены сечения сигнального процесса
Планы
- Определить систематические ошибки
- Представить результаты работы на конференциях и т.д.
- Совместный анализ с e+e– ➝ K+K–